AULA 2 – Matemática – 5º Ano – 2º CORTE - 27/05/2020
Vamos iniciar mais uma aula!

Muita atenção! Vamos lá!!!
O assunto de hoje é:
Operações inversas a partir de igualdades
Em toda igualdade, podemos fazer interpretações usando operações inversas, mantendo verdadeira a igualdade.
Por exemplo, 5 + 4 = 9, nos fazem concluir também que:
a) 5 = 9 – 4
b) 4 = 9 – 5
Isso ocorre por causa das propriedades da igualdade, a saber:
1. Toda igualdade se mantém, ao adicionarmos ou subtrairmos uma mesma quantidade de ambos os lados da igualdade.
2. Toda igualdade se mantém, ao multiplicarmos ou dividirmos uma mesma quantidade de ambos os lados da igualdade.
Exceto para o número zero, pois não existe divisão por zero.
Em nosso exemplo, a partir da igualdade 5 + 4 = 9,
a) se subtrairmos 4 dos dois lados obtemos 5 = 9 – 4;
b) se subtrairmos 5 dos dois lados obtemos 4 = 9 – 5.
Propriedades da Igualdade.
Seja um valor numérico desconhecido em uma igualdade. Este valor numérico desconhecido recebe o nome de incógnita.
Exemplo 1.
Em uma igualdade, se queremos eliminar um número que está sendo adicionado, devemos subtrair esse número dos dois lados para que a igualdade permaneça.
Veja que para descobrir o valor da incógnita, será preciso eliminar o número 100 que está sendo adicionado a ele. Assim, para que a igualdade permaneça, deve-se subtrair 100 dos dois lados, como segue:
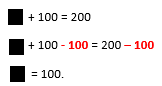
Exemplo 2.
Em uma igualdade, se queremos eliminar um número que está multiplicando, devemos dividir os dois lados por esse número para que a igualdade permaneça.
Veja que para descobrir o valor da incógnita, será preciso eliminar o número 4 que está multiplicando-o. Assim, para que a igualdade permaneça, deve-se dividir os dois lados por 4, como segue:
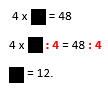
Noção de equivalência em igualdades.
Em todas as igualdades podemos somar ou subtrair a mesma quantidade em ambos os lados, como também multiplicar ou dividir pela mesma quantidade os dois membros, desde que seja uma quantidade diferente de zero. Essas propriedades das igualdades permitem estabelecer equivalências nos cálculos, facilitando a compreensão mesmo em problemas desafiadores, como os famosos desafios matemáticos figurados do WhatsApp.
Observe o desafio figurado a seguir:

Qual seria o valor da maçã?
Nesta igualdade ao retirarmos uma pêra, uma maçã e 7 de cada lado, obtemos uma igualdade equivalente mais fácil de analisar.
Veja:
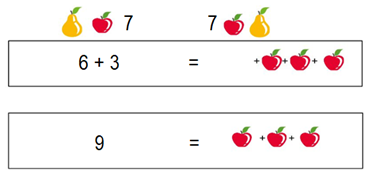
De um lado da igualdade teremos o 9, e do outro lado, três maçãs. Assim, dividindo-se ambos os lados por 3, temos que cada maçã equivale a 3. Logo, se cada maça equivale a 3, então:
3 + 3 + 3 =9
Agora é sua vez!
Responda as atividades a seguir no seu caderno
1. Complete os quadros A, B, C, D, E no circuito a seguir, com os números que satisfazem as operações indicadas pelas setas:
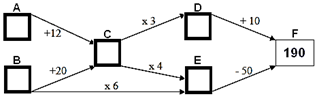
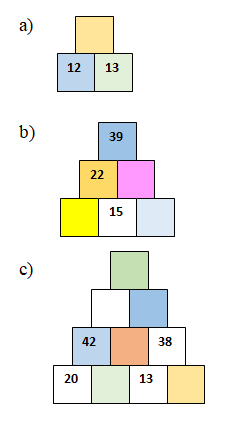
2. Uma pirâmide é numérica se o valor de um quadradinho for igual à soma dos dois quadradinhos logo abaixo. Sabendo que as pirâmides a seguir são numéricas, calcule o valor dos quadradinhos abaixo.
3. Calcule o valor da incógnita em cada caso:
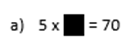
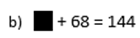
4. Observe a imagem a seguir:
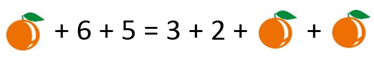
Qual é o valor de cada laranja?
(a) 2
(b) 3
(c) 5
(d) 6
5. Observe a tabela a seguir:
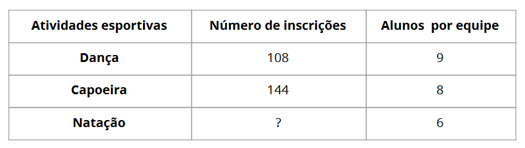
Sabendo que o total de alunos inscritos é 324, responda:
a) Qual é o número de inscrições para Natação?

b) Quais atividades esportivas têm a mesma quantidade de equipes, ao dividir o número de inscrições pela quantidade de alunos por equipe?
6. Eu tenho 10 anos. Minha irmã tem metade da minha idade. Meu pai tem o triplo da soma da minha idade com a idade da minha irmã. Minha mãe é 10 anos mais jovem que meu pai. Então, a idade da minha mãe é:

(a) 25 anos
(b) 30 anos
(c) 35 anos
(d) 40 anos
7. Observe a imagem a seguir:
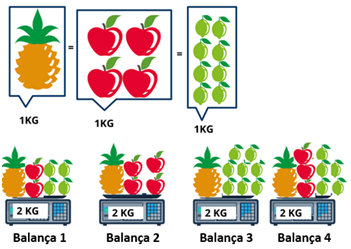
Qual das balanças está com marcação errada?
(a) Balança 1
(b) Balança 2
(c) Balança 3
(d) Balança 4
8. O sucessor do número 8 é triplo de um número. Esse número é __________.
9. O dobro de um número é o antecessor de 15. Esse número é ____________.

Nossa aula chegou ao fim.
Mas não se esqueça:

















Aulas muito boas