Vamos iniciar nossa aula!!!

No nosso cotidiano utilizamos muito os números racionais. Veja os exemplos na receita de bolo a seguir:

Observe que em qualquer fração temos, o número de cima que é o numerador e o número de baixo que é o denominador.

O numerador indica o número de partes iguais em que o inteiro (todo) foi dividido já o denominador indica quantas dessas partes foram consideradas.

Existem diversos significados para as frações:

Representação de uma ou mais partes de algo que foi dividido em partes iguais;

– Representação de uma divisão, em que o numerador equivale ao dividendo e o denominador equivale ao divisor;

– Representação de um número racional.

Frações equivalentes e simplificação

Frações equivalentes são aquelas que representam o mesmo número racional. Isso significa que elas possuem o mesmo valor. Por exemplo:

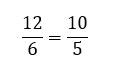
Ambas as frações representam o número inteiro 2.

Para encontrar frações equivalentes, basta multiplicar o numerador e o denominador de uma fração pelo mesmo número (pode ser qualquer número, a não ser que o problema exija algum específico). Por exemplo:

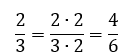
Como o numerador e o denominador foram multiplicados pelo mesmo número, as frações dois terços e quatro sextos são equivalentes.

O processo de divisão pelo mesmo número também pode ser utilizado para encontrar frações equivalentes. Quando esse processo é utilizado, dizemos que a fração foi simplificada. Por exemplo:

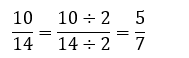
Frações e decimais.

Em geral, transforma-se uma fração decimal em um número decimal fazendo com que o numerador da fração tenha o mesmo número de casas decimais que o número de zeros do denominador. Na verdade, realiza-se a divisão do numerador pelo denominador.

Exemplos:

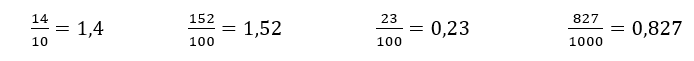
Se o denominador for diferente de 10, 100, 1000, etc, dividimos o numerador pelo denominador:

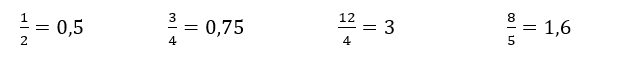
Também é possível transformar um número decimal em uma fração decimal. Para isto, toma-se como numerador o número decimal sem a vírgula e como denominador a unidade (1) seguida de tantos zeros quantas forem as casas decimais do número dado. Como exemplo, temos:

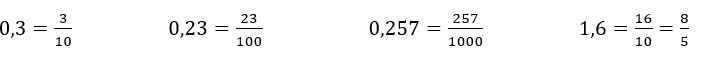
Comparação de números racionais.

Para fazer a comparação de números racionais, podemos utilizar a reta numérica. Dessa forma, fica mais fácil e evidente a diferenciação entre os números.

 Para fazer a comparação de números racionais, podemos utilizar a reta numérica. Dessa forma, fica mais fácil e evidente a diferenciação entre os números.

Exemplo:

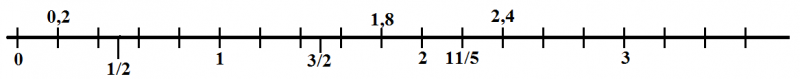
Fração e Porcentagem

A palavra porcentagem apresenta ligações estreitas com a ideia de fração, uma vez que significa partes de 100. Ora, se é parte de um todo então é uma fração. Vamos compreender melhor a relação entre porcentagem e as frações através dos exemplos a seguir:

Como a porcentagem pode ser escrita na forma de fração, podemos realizar facilmente cálculos que envolvam essas ideias. Exemplo:

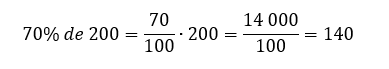
Chegou a hora de realizar as atividades. Vamos lá!!!

Lápis e caderno na mão e muito capricho.

1. Um médico deve trabalhar 40 horas semanais. Devido a um acúmulo de serviço na semana passada, ele precisou fazer 12 horas extras. A fração que corresponde a quanto ele trabalhou a mais do que o previsto é

a) (  ) 1/4.

b) (  ) 1/5.

c) (  ) 2/5.

d) (  ) 3/

2. Observe a figura:

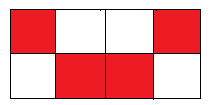
a) Em quantas partes iguais o retângulo foi dividido?

b) Cada uma dessas partes representa que fração do retângulo?

c) A parte pintada representa que fração do retângulo?

3. Escreva como se lê:

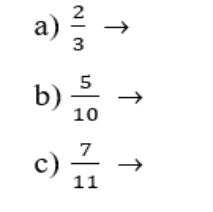
4. Marlene fez um bolo e convidou suas amigas para lanchar. O bolo foi dividido em seis fatias iguais. Cada menina comeu 2 fatias. A fração do bolo que cada menina comeu é

5. Qual é a fração irredutível da fração obtida no exercício anterior?

6. Em cada retângulo, pinte as partes correspondentes às frações e responda:

Qual é a maior fração? _________

 7. Pinte a parte correspondente à fração indicada e responda:

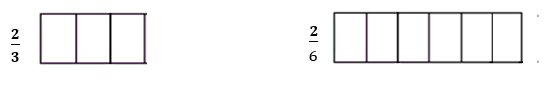
Qual é a maior fração? _________

 8. Complete as frações para que sejam equivalentes:

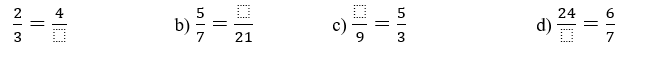
9. Transforme cada decimal a seguir em sua representação fracionária:

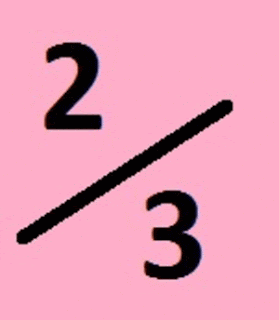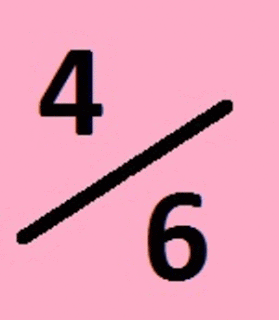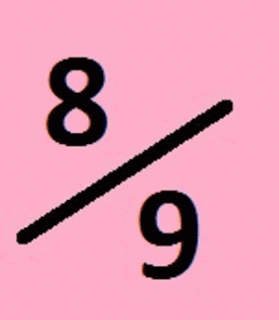
10. Transforme cada fração a seguir em sua representação decimal:

11. Calcule as porcentagens abaixo:

a) 40% de 150

b) 50% de 70

Chegamos ao final das atividades.