A atividade hoje será sobre:

Comprimento

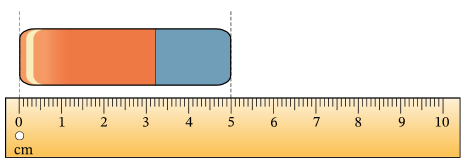
É a grandeza associada à extensão longitudinal entre dois pontos. Em termos mais simples, é a grandeza que pode ser medida, calculando-se a distância entre dois pontos dados e comparando com uma unidade de medida, que pode ser padronizada ou não padronizada. Na imagem a seguir, é feita a medida do comprimento de uma borracha, comparando a extensão longitudinal de suas extremidades com a unidade de medida centímetro. Após essa comparação, concluímos que o comprimento da borracha é de 5 centímetros.

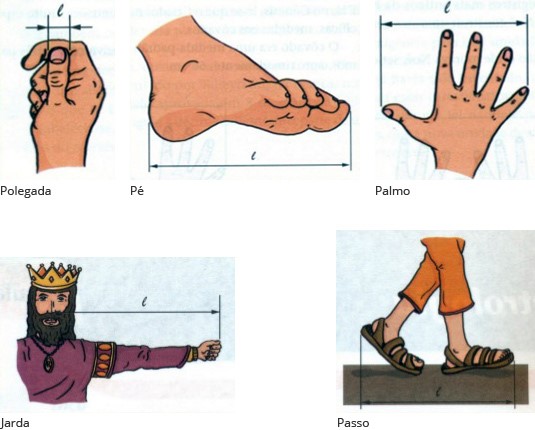
Entre as unidades de medida usadas para medir comprimentos, temos aquelas que são não padronizadas como o pé, o palmo, o passo, a polegada, a milha, a légua e a jarda, por exemplo. Essas medidas variam de pessoa para pessoa, não tem um valor fixo. No entanto, elas oferecem estimativas quando não dispomos de instrumentos padronizados para medir, como uma régua.

Suponha que para medir o comprimento de uma sala, o pé seja a unidade de medida escolhida. Como as dimensões dos pés variam de pessoa para pessoa, então a medida observada será diferente de pessoa para pessoa. Imagine um pé “grande”,  de numeração 45, e um pé “pequeno”, de numeração 30. Para uma medida correspondendo a uma numeração 900, seriam necessários 20 pés grandes , e seriam necessários 30 pés pequenos . E agora, são 20 pés ou 30 pés?

Para resolver este problema, foram estabelecidos valores aproximados que servem para a conversão das medidas não padronizadas em medidas padronizadas usuais como milímetro, centímetro, metro ou quilômetro. Por exemplo, uma jarda mede aproximadamente 0,91 metros e uma milha tem aproximadamente 1609 metros.

No quadro a seguir temos o metro (m), seus múltiplos – quilômetro (km), hectômetro (hm) e decâmetro (dam) – e submúltiplos – decímetro (dm), centímetro (cm) e milímetro (mm), que são as medidas padronizadas de comprimento. Observe:

Transformações de medidas de comprimento – Método Escada

Para transformar as medidas de comprimento, podemos proceder usando multiplicações ou divisões sucessivas por 10, conforme o esquema a seguir, que simula a transformação com a analogia de subidas ou descidas de degraus em uma escada – Método Escada.

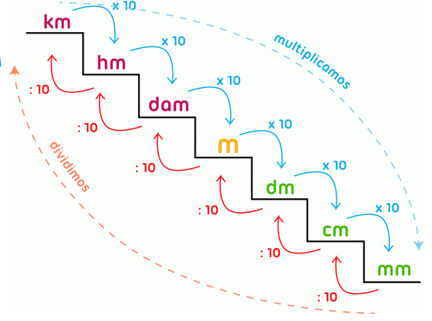
Por exemplo, se a medida é  centímetros (cm) e desejamos obter a medida equivalente em metros (m), então é preciso subirmos dois degraus. Esta subida significa dividir por 10 duas vezes consecutivas. Como  : 10 = 240 e 240 : 10 = 24, segue que  centímetros equivalem a 24 metros.

Se queremos transformar uma medida de 5 quilômetros (km) para metros (m), então observamos que será necessário descer 3 degraus. Esta descida significa multiplicar por 10 três vezes consecutivas. Como 5 x 10 x 10 x 10 = , segue que 5 quilômetros equivalem a metros.

Indicamos a seguir, um applet para você interagir com as medidas de comprimento. Siga as instruções e complete os desafios. Bons estudos!!!

Interação – O longo e o comprido à https://tinyurl.com/yywlzk2q

Chegou a hora de realizar as atividades

Leia atentamente a tirinha da Turma da Mônica a seguir para responder as atividades 1, 2 e 3.

1. Cebolinha troca o R por L e diz “Légua” quando queria dizer “Régua”. Sabendo que uma légua mede 6 km, qual é a distância equivalente a 7 léguas?

Cálculo:

Resposta:_____________________________________________________

2. Mônica tinha razão: sete Léguas é uma distância muito maior do que estavam em relação ao poste naquele instante. Qual seria a unidade de medida mais apropriada para medir aquela distância?

__________________________________________________________________________

3. Cebolinha utiliza 7 réguas de 30 cm de comprimento para mostrar que tinha razão, quanto ao comprimento que ele sugeriu. Qual é a medida que se obtém com estas 7 réguas?

Cálculo:

Resposta:____________________________________________________

4. Em um jogo de golfe, Sérgio se encontra a 300 jardas do primeiro buraco do jogo e se prepara para a tacada. Adotando a medida de 100 jardas como 91 metros, qual é a distância equivalente para essa tacada em metros?

Cálculo:

Resposta:__________________________________________________

5. Observe a imagem a seguir.

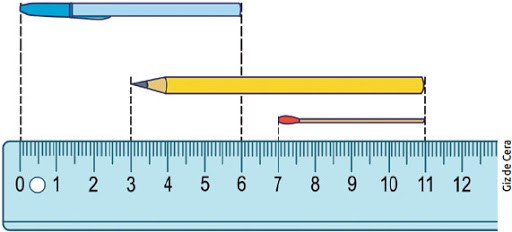
As medidas em centímetros dos comprimentos da caneta, do lápis e do fósforo, respectivamente, são

a) (  ) 6, 8 e 4.

b) (  ) 6, 9 e 5.

c) (  ) 6, 10 e 3.

d) (  ) 6, 11 e 11.

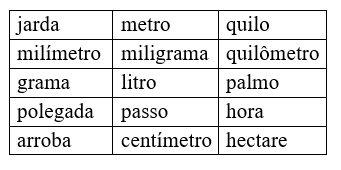
6. Pinte as palavras do quadro a seguir, que são  usadas como medidas de comprimento.

7. Observe a ilustração a seguir.

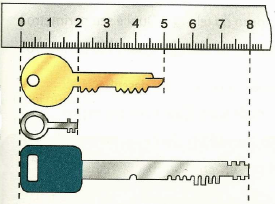
Qual a diferença de comprimento entre a chave maior e a chave menor?

a) (  ) 2 cm.

b) (  ) 3 cm.

c) (  ) 6 cm.

d) (  ) 8 cm.

8. O comprimento de uma mesa é de 88 cm. Sabe-se que um palmo é uma medida de comprimento que tem aproximadamente 22 cm.

Quantos palmos são necessários para medir essa mesa?

a) (  ) 5

b) (  ) 4

c) (  ) 3

d) (  ) 2

9. Uma milha terrestre mede pouco mais de 1600 m.

Qual é a medida que mais se aproxima de 5 milhas terrestres?

a) (  ) 2 km

b) (  ) 4 km

c) (  ) 8 km

d) (  ) 16 km

10. Leia atentamente os diálogos a seguir.

Nesses diálogos vimos algumas situações em que podemos empregar as medidas de comprimento.

a) Para cada uma das medidas de comprimento a seguir, estabeleça pelo menos uma situação em que ela é usada.

polegadas:____________________________________________________

milímetros:___________________________________________________

quilômetros:_________________________________________________

pés:___________________________________________________________

metros:______________________________________________________

centímetros:__________________________________________________

milhas:_______________________________________________________

b) Complete as lacunas, realizando a transformação de medidas de comprimento em cada caso:

8 km = ______ metros.

500 cm = ______ milímetros.

2 500 m = ______ decâmetros.

600 dam = ______ quilômetros.

Chegamos ao

QUER APRENDER MAIS? BAIXE O AQUIVO COMPLETO DA ATIVIDADE, VOCÊ PODERÁ IMPRIMIR OU COPIAR NO SEU CADERNO

Atividade-3-Tema-Medidas-de-comprimento-padronizada-e-nao-padronizada-3o-ano

Até a próxima atividade!!!