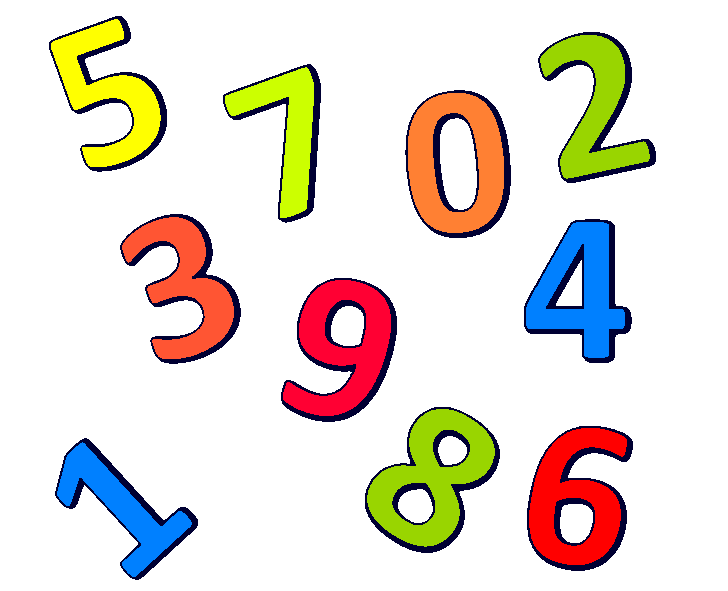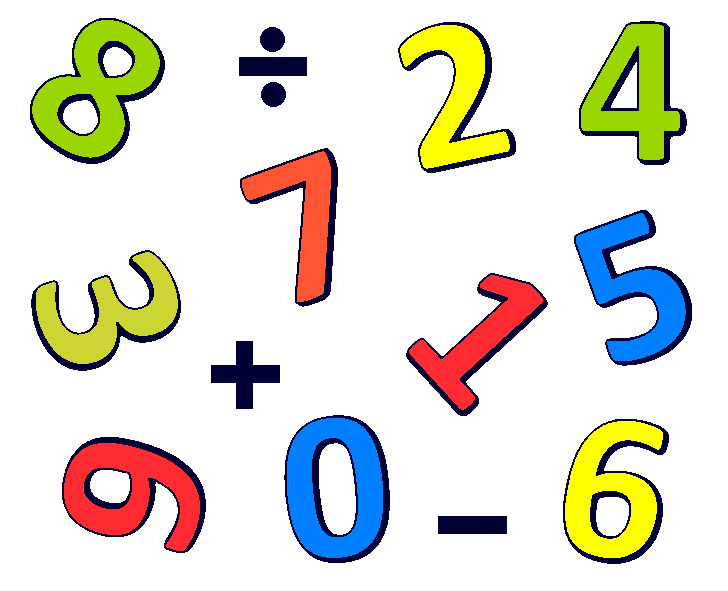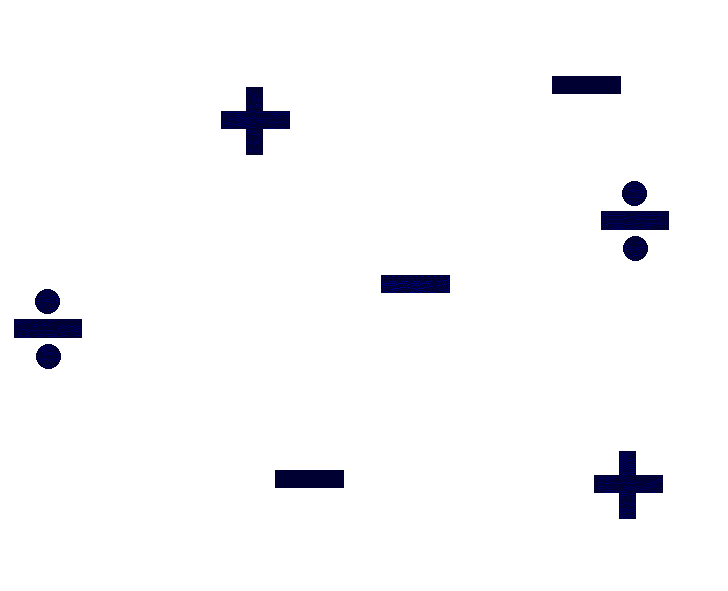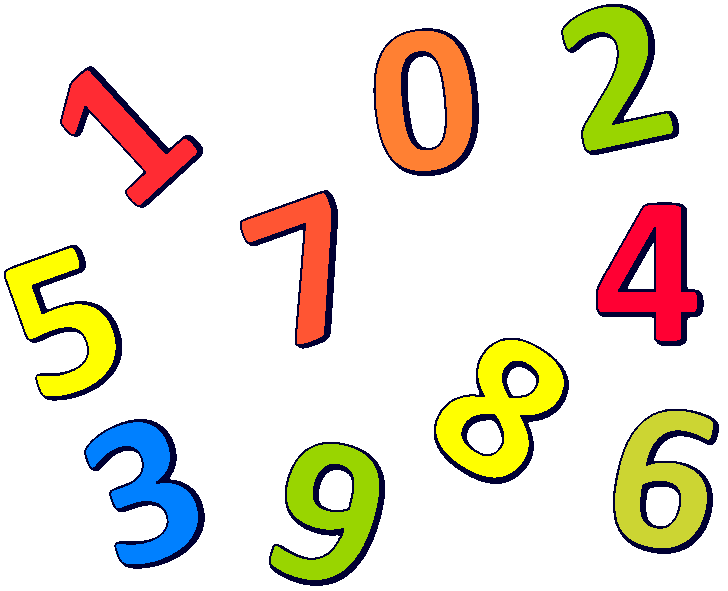OLÁ PESSOAL!

Experimento aleatório: É um experimento que, repetido várias vezes de forma semelhante, apresenta resultados imprevisíveis. Por exemplo, o lançamento de uma moeda. Sabemos que pode sair cara ou coroa ao lançarmos uma vez, mas não podemos garantir, com exatidão, as quantidades de caras e de coroas que sairão em 10 lançamentos.

Espaço amostral: É o conjunto de todos os resultados possíveis de ocorrer em um experimento aleatório. Para compreender melhor esse conceito, vamos explorar alguns exemplos.

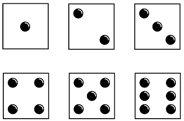
Exemplo 1. Lançamento de um dado.

O experimento aleatório “lançar um dado de 6 faces e anotar a face voltada para cima”, tem 6 possíveis resultados. Veja:

Dizemos que o espaço amostral desse experimento tem 6 possibilidades. Considere que, nesse experimento, Augusto lance o dado e diga que o resultado será um número par, enquanto sua amiga Alice acredita sair um número que divide 6. Qual destes palpites apresentados tem mais chances de ocorrer?

Dentre os 6 possíveis resultados {1, 2, 3, 4, 5, 6} desse espaço amostral, temos 3 números pares {2, 4, 6} e 4 números que dividem 6 {1, 2, 3, 6}. Logo, temos 3 de 6 resultados possíveis de sair um número par e 4 de 6 resultados possíveis de sair um número que divide 6. Portanto, dizemos que no lançamento de um dado, o palpite de Alice é mais provável do que o de seu amigo Augusto.

No entanto, essa previsão pode não se confirmar imediatamente no primeiro lançamento e, mesmo com menor chance, Augusto pode acertar e vencer a disputa dos palpites, ou ainda, sair o número 5 e ambos errarem seus palpites. Esse fato é o que caracteriza o experimento aleatório, pois não podemos dizer com precisão, quantas vezes Alice ou Augusto vão acertar, ao repetirem o experimento.

O que podemos fazer é estimar, pelo estudo do espaço amostral, que Alice tem mais chances de vencer, quanto maior a frequência de repetições desse experimento. Além disso, podemos estimar que a chance de nenhum deles vencer é bem menor do que a chance de algum de seus palpites ser contemplado, uma vez que apenas 1 dos 6 resultados possíveis é desfavorável a ambos os palpites, a saber, o número 5.

Dessa forma, compreendemos que o espaço amostral nos dá uma visão geral dos resultados possíveis para fazermos uma previsão de resultados desejados, como os palpites dados por Augusto e Alice, e dos resultados desfavoráveis no experimento, como o eventual lançamento do número 5, a fim de tomarmos uma decisão.

Exemplo 2. Lançamento de duas moedas.

O experimento aleatório “lançar duas moedas, uma de 10 centavos e outra de 25 centavos, anotando a face voltada para cima” tem o seguinte espaço amostral: cara na moeda de 10 centavos e cara na moeda de 25 centavos; coroa na moeda de 10 centavos e coroa na moeda de 25 centavos; cara na moeda de 10 centavos e coroa na moeda de 25 centavos; e coroa na moeda de 10 centavos e cara na moeda de 25 centavos. Observe:

Atividades

Leia atentamente a tirinha a seguir, para responder as atividades 1, 2 e 3.

1. Lançar um dado de 20 faces numeradas de 1 a 20, anotando o número que aparece na face superior central como na tirinha é um experimento aleatório? Se a resposta for positiva, indique o espaço amostral desse experimento. ________________________________________________________________________________________________________________________________________________

2. Se Caco tivesse escolhido um número ímpar maior do que 6, qual seria a medida da chance de ele ganhar, considerando o espaço amostral? ________________________________________________________________________________________________

3. Após o diálogo, Caco experimenta escolher um número que divide um número par de qualquer uma das faces. Como você classifica a medida da chance de ele acertar esse palpite?________________________________________________________________________________________________

4. Observe o espaço amostral do lançamento de dois dados de 6 faces a seguir. ________________________________________________________________________________________________

Nesse experimento aleatório, a escrita (5,3) significa que o primeiro dado teve como resultado 5 e o segundo dado teve como resultado 3. Nessas condições, complete as lacunas no texto a seguir:

Ao lançar dois dados de 6 faces e anotar o resultado em suas faces superiores, obtemos um espaço amostral com ______ resultados possíveis.

O resultado (2, 6) significa que o primeiro dado resultou em ____ e que o segundo dado resultou em _____. Se Daniela escolher que os números do lançamento dos dois dados devem ser iguais, ela tem _____ chances de acertar dentre os ______ possíveis resultados.

Fátima lançou os dois dados e disse que a soma dos números desses dois dados seria menor do que 5, e com sorte venceu, apesar do resultado ser pouco provável. Isso ocorre pois os lançamentos de dois dados com soma menor do que 5 acontecem apenas nos seguintes casos: (1,1); (1,2); (__, __) e (__, __), ou seja, Fátima acerta o palpite em ______ dentre os ______ resultados possíveis.

5. Considere o experimento aleatório a seguir. ________________________________________________________________________________________________

Lançar três moedas e anotar a face voltada para cima, usando a letra C se a face for “cara” ou a letra K se a face for “coroa”.  Alguns dos possíveis resultados são as três moedas terem faces iguais como em (C, C, C)  e (K, K, K).

Complete o espaço amostral desse experimento, apresentando todos os 8 possíveis resultados.

(C, C, C); (K, K, K); (__, ___, __); (__, ___, __); (__, ___, __); (__, ___, __); (__, ___, __);(_, __, __).

6. Analise as descrições a seguir.

Descrição 1: Lançar uma moeda e sair coroa – Impossível.

Descrição 2: Lançar um dado de 6 faces e sair 7 – Impossível.

Descrição 3: O Sol irá nascer a leste amanhã – Acontecerá.

Descrição 4: O aniversário da primeira pessoa que encontrar amanhã é 30 de fevereiro – Pode acontecer.

Pode-se afirmar que estão corretas as descrições

a) (  ) 1 e 3.

b) (  ) 1 e 4.

c) (  ) 2 e 3.

d) (  ) 2 e 4.

7. Observe a ilustração a seguir.

Qual é a quantidade total de resultados possíveis ao lançar estes dois objetos ao mesmo tempo?

a) (  ) 2

b) (  ) 6

c) (  ) 8

d) (  ) 12

8. A expressão EQUIPROVÁVEL se refere a resultados que tem a mesma chance de ocorrer em um experimento aleatório. Considere que uma cesta de frutas tenha 4 maçãs, 5 peras, 5 bananas e 11 ameixas.

Ao escolher uma fruta desta cesta, quais das seguintes frutas escolhidas são equiprováveis?

a) (  ) maçã e banana

b) (  ) pera e banana

c) (  ) ameixa e maçã

d) (  ) ameixa e pera

9. O mês de maio tem 31 dias. Gustavo escolheu aleatoriamente uma data do mês de maio de 2021, sem consultar um calendário.

Essa data pode

a) (  ) cair em um final de semana em 10 dos 31 resultados possíveis.

b) (  ) cair em um feriado em 8 dos 31 resultados possíveis.

c) (  ) ser uma terça-feira em 6 dos 31 resultados possíveis.

d) (  ) ser uma segunda-feira em 4 dos 31 resultados possíveis.

10. Eliane tem as 26 letras de nosso alfabeto em fichas guardadas numa urna e pede que seu aluno Mário retire uma ficha aleatoriamente.

Para a ficha retirada ser uma vogal temos

a) (  ) 10 dentre os 26 resultados possíveis.

b) (  ) 8 dentre os 26 resultados possíveis.

c) (  ) 5 dentre os 26 resultados possíveis.

d) (  ) 4 dentre os 26 resultados possíveis.

QUER APRENDER MAIS? BAIXE O ARQUIVO COMPLETO DA ATIVIDADE, VOCÊ PODERÁ IMPRIMIR OU COPIAR NO SEU CADERNO.