A nossa aula de hoje será sobre Frações.

Então vamos lá!

Frações

É um modo de representar as partes pelas quais um objeto foi dividido.

Todo “objeto original” que não tenha sido dividido é chamado de inteiro.

Ao fazer cortes nesse objeto, estamos dividindo-o. Se a divisão resultar em partes iguais, é possível representar esse objeto por meio de frações.

A palavra FRAÇÃO vem de uma palavra do latim que significa “quebrar”.

Uma fração é chamada de fração comum quando os números (ou termos) são escritos um sobre o outro, separados por uma barra ou linha.

Por exemplo:   

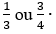
Na figura a seguir, a fatia representa uma fração da pizza inteira:

Veja a seguir o que significam os dois números que aparecem nas frações:

IMPORTANTE

Qualquer número pode ser um numerador.

Qualquer número com exceção do zero pode ser um denominador.

Representando frações

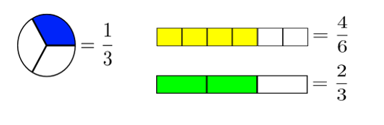
TIPOS DE FRAÇÃO

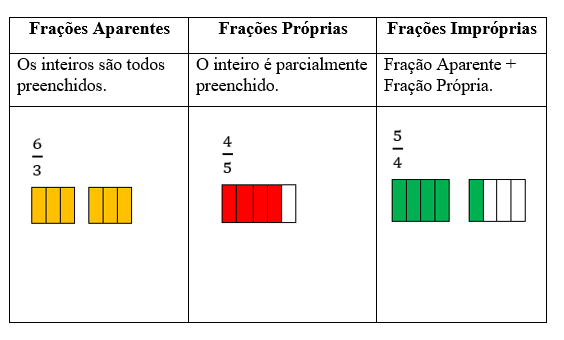
FRAÇÕES APARENTES

Se a divisão dos dois números apresentados na fração resulta em um número natural, dizemos que a fração é aparente.

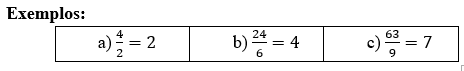
 Note que em todos esses casos, o numerador é múltiplo do denominador.

FRAÇÕES PRÓPRIAS

Se a divisão dos dois números apresentados na fração resulta em um número entre 0 e 1, dizemos que a fração é própria.

Note que em todos esses casos, o numerador é menor do que o denominador.

FRAÇÕES IMPRÓPRIAS

Se a divisão dos dois números apresentados na fração resulta em um número maior que 1 e não natural, dizemos que a fração é imprópria.

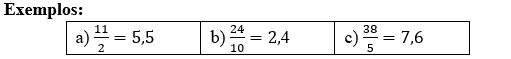
Note que em todos esses casos, o numerador é maior do que o denominador.

A tabela a seguir mostra como se comportam essas frações graficamente.

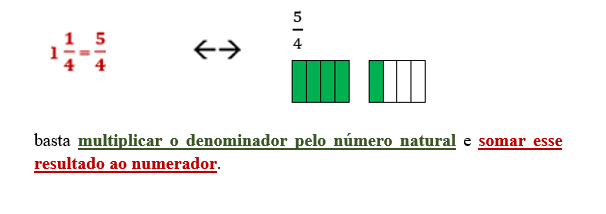
NÚMEROS MISTOS

São números escritos com duas representações: um número natural (fração aparente) acompanhado de uma fração própria.

Veja a seguir uma situação envolvendo um número misto:

ATENÇÃO PARA ESSA RECEITA

Números mistos podem ser escritos na forma de uma fração imprópria.

Veja:

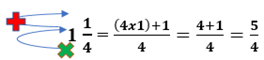
Representação de frações e decimais na reta numérica

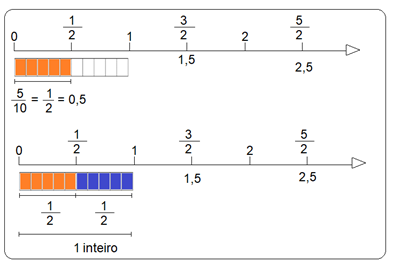
Leitura de números decimais

Toda fração pode ser interpretada como a divisão do numerador pelo denominador.

O resultado dessa divisão é representado pelo que chamamos de número decimal.

O número natural, à esquerda da virgula deverá ser lido com o acréscimo da palavra “inteiro” ou ainda “inteiros”.

A cada ordem após a vírgula lemos décimos, centésimos, milésimos, décimos de milésimos e assim por diante. Se a quantidade de algarismos após a vírgula for finita, lemos o número (composto por todos os algarismos após a vírgula) acrescido da palavra que representa a última ordem decimal para a direita.

Veja:

Interpretação

* 1 antes da vírgula: um inteiro

* à 125 depois da vírgula, última ordem decimal para a direita é milésimos: cento e vinte e cinco milésimos.

Leitura:

Um inteiro e cento e vinte e cinco milésimos.

Observe que, se o número antes da vírgula for zero, lê-se apenas a parte decimal.

Veja:

Chegou a hora de revolver as atividades a seguir:

E colocar o cérebro para exercitar!

1. Observe o desenho a seguir e responda.

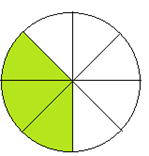
Em quantas partes, o círculo foi dividido?

Quantas são as partes brancas marcadas ?

Que fração indica a quantidade de partes brancas em relação ao total de partes?

Na fração, qual é o numerador? E o denominador?

Faça a representação gráfica de cada uma das frações a seguir, conforme o exemplo:

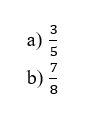
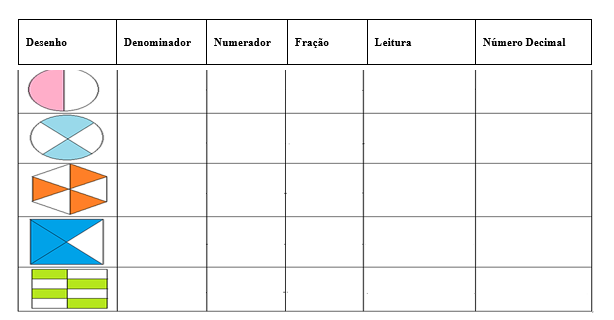
Complete o quadro a seguir com o que se pede:

Escreva como se lê cada fração a seguir:

É isso aí vamos continuar!

Olha que delícia!

Observe a receita de Cupcake, na imagem a seguir:

Copie no seu caderno as frações impróprias que correspondem às porções das xícaras de açúcar refinado, farinha de trigo e de leite.

A nossa aula já terminou!

Quer aprender mais? Acesse o link abaixo faça o download da atividade.

Você poderá imprimir ou copiar no seu caderno.

E NÃO SE ESQUEÇAM…