ATIVIDADE 17 – Dízima periódica e fração geratriz. - 07/10/2021
Dízima Periódica e fração geratriz.
O número 0,333… é chamado de decimal periódico não exato (dízima periódica), e sendo um número racional, podemos associar esse número a uma fração, denominada de fração geratriz. Logo, toda dízima periódica, deve possuir uma forma fracionária. Temos dois tipos de dízima periódica.
I) Dízima periódica simples: o período (algarismo ou algarismos que se repetem) começa a partir da virgula.
Exemplos:
0,3333…, período 3 (período com um algarismo)
0,232323…, período 23 (período com dois algarismos)
1,123123…, período 123 (período com três algarismos)
II) Dízima periódica composta: antes do período começar, existem números que não fazem parte do período (Chamamos de antiperíodo).
0,5333…, período 3 e antiperíodo 5.
0,15666… período 6 e antiperíodo 15
2,123646464… período 64 e antiperíodo 123
Para determinarmos uma fração geratriz vamos seguir os seguintes passos:
Dízima periódica simples:
1º passo: Igualar a dízima periódica a uma incógnita, por exemplo x, de forma a escrever uma equação do 1º grau com uma incógnita.
2º passo: Multiplicar ambos os lados da equação por um múltiplo de 10. Para descobrir qual será o múltiplo, devemos identificar quantos casas decimais devemos “andar” para que o período fique antes da vírgula.
3º passo: Subtrair da equação encontrada, a equação inicial.
4º passo: Resolver a equação obtida no 3º passo.
Exemplo. Determine a fração geratriz do número 0,777…
1º passo: Igualar a dízima periódica a uma incógnita de forma a escrever uma equação do 1º grau:
2º passo: Multiplicar ambos os lados da equação por um múltiplo de 10. Para descobrir qual será o múltiplo, devemos identificar quantos casas decimais devemos “andar” para que o período fique antes da vírgula.
3º passo: Subtrair da equação encontrada, a equação inicial.
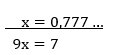
4º passo: Resolver a equação obtida no 3º passo.
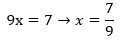
Este processo pode ser simplificado seguindo a seguinte regra: coloca-se o período no numerador da fração e, para cada algarismo dele, coloca-se um algarismo 9 no denominador. Essa regra se a dízima for menor do que 1. Se for maior que 1, separamos a parte inteira e depois adicionamos a fração encontrada:
Menor do que 1:
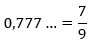
Se for maior do que 1:
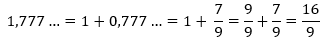
Dízima periódica composta:
1º passo: Igualar a dízima periódica a uma incógnita, de forma a escrever uma equação do 1º grau com uma incógnita.
2º passo: Multiplicar ambos os lados da equação por um múltiplo de 10, observando a quantidade de casas do antiperíodo. Depois repetir o mesmo processo da dízima periódica simples.
3º passo: Subtrair da última equação encontrada, a penúltima equação.
4º passo: Resolver a equação obtida no 3º passo.
Exemplo: Determine a fração geratriz do número 0,2333…
1º passo: Igualar a dízima periódica a uma incógnita, de forma a escrever uma equação do 1º grau.
2º passo: Multiplicar ambos os lados da equação por um múltiplo de 10, de modo que o antiperíodo fique antes da vírgula. Depois, obter outra equação, multiplicando por um múltiplo de 10 também, de modo que o antiperíodo e o período fiquem antes da vírgula.
3º passo: Subtrair da última equação encontrada, a penúltima equação.
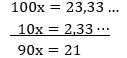
4º passo: Resolver a equação obtida no 3º passo
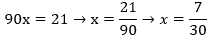
Este processo pode ser simplificado seguindo a seguinte regra: Aqui, a dica é um pouco diferente: para cada algarismo do período ainda se coloca um algarismo 9 no denominador. Mas, agora, para cada algarismo do antiperíodo se coloca um algarismo zero, também no denominador. No caso do numerador, faz-se a seguinte conta: (parte inteira com antiperíodo e período) – (parte inteira com antiperíodo)
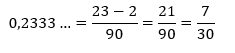
Para saber mais, se possível, assista ao vídeo
ATIVIDADES:
1. Expresse na forma de fração os seguintes números racionais
a) 0,777….
b) 1,3232….
c) 1,444….
d) 0,033…
e) 2,35111…
2. Apresente o resultado da expressão na forma fracionária:
0,66666… + 0,25252525… – 0,77777…
3. O número real representado por 0,5222… é
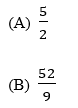
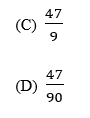
4. (Ufrgs 2008-adaptado) Se x = 0,949494… e y = 0,060606…, então x + y é igual a
(A) 1,01.
(B) 1,11.
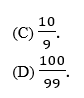
5. (Pucrj 2007) Escreva na forma de fração a soma 0, 2222… + 0, 23333….
6. (Pucrj 2004) A soma 1,3333… + 0,16666… é igual a:
(A) 1/2
(B) 5/2
(C) 4/3
(D) 3/2
7. (Ufrj 2002) Sejam e (dízima periódica). Quais das afirmações a seguir são verdadeiras?
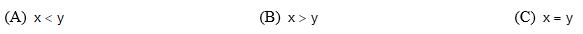
Justifique sua resposta.
8. Dos números a seguir, assinale aquele que corresponde a uma dízima periódica composta.
(A) 3,14159284…
(B) 2,21111
(C) 0,3333….
(D) 1,21111….
