Números racionais/Dízima periódica – Atividade 2 - 09/02/2021

Números racionais – Dízima Periódica
O número 0,333… é chamado de decimal periódico não exato (dízima periódica), portanto podemos associar esse número a uma fração, denominada de fração geratriz. Logo, toda dízima periódica, deve possuir uma forma fracionária. Temos dois tipos de dízima periódica
I) Simples: o período começa a partir da virgula;
a) 0,2222…, período 2 (um algarismo)
b) 0,353535…, período 35 (dois algarismos)
c) 2,123123…, período 123 (três algarismos)
II) Composta: antes do período começar existem números denominados de antiperíodo que não fazem parte do período.
a) 0,3222…, período 2 e antiperíodo 3
b) 1,20333… período 3 e antiperíodo 20
c) 0,012515151… período 51 e antiperíodo 012
Para determinarmos uma fração geratriz vamos seguir os seguintes passos
1º passo: Igualar a dízima periódica a uma incógnita, por exemplo x, de forma a escrever uma equação do 1º grau.
2º passo: Dízima periódica simples – multiplicar ambos os lados da equação por um múltiplo de 10. Para descobrir qual será o múltiplo, devemos identificar quantos casas decimais devemos “andar” para que o período fique antes da vírgula. Dízima periódica composta multiplicar ambos os lados da equação por um múltiplo de 10, observando a quantidade de casas do antiperíodo. Depois repetir o mesmo processo da dízima periódica simples.
3º passo: Dízima periódica simples – diminuir a equação encontrada da equação inicial. Dízima periódica – diminuir a última equação encontrada da penúltima e isolar a incógnita.
Exemplo. Determine a fração geratriz do número 0,222…
1º passo: Igualar a dízima periódica a uma incógnita, por exemplo x, de forma a escrever uma equação do 1º grau.
x=0,222...
2º passo: Dízima periódica simples – multiplicar ambos os lados da equação por um múltiplo de 10. Para descobrir qual será o múltiplo, devemos identificar quantos casas decimais devemos “andar” para que o período fique antes da vírgula. Dízima periódica composta multiplicar ambos os lados da equação por um múltiplo de 10, observando a quantidade de casas do antiperíodo. Depois repetir o mesmo processo da dízima periódica simples.
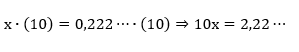
3º passo: Dízima periódica simples – diminuir a equação encontrada da equação inicial. Dízima periódica – diminuir a última equação encontrada da penúltima e isolar a incógnita.
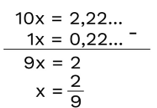
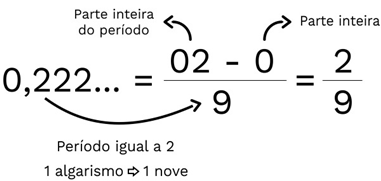
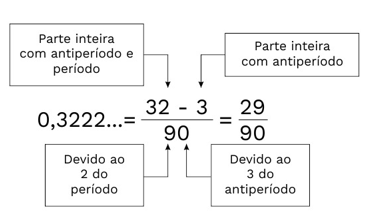
Será que podemos simplificar esse processo? Temos um método prático para encontrar a fração geratriz. Observe a imagem abaixo
Exemplo 02. Determine a fração geratriz do número 0,3222…
1º passo: Igualar a dízima periódica a uma incógnita, por exemplo x, de forma a escrever uma equação do 1º grau.
x= 0,3222…
2º passo: Dízima periódica simples – multiplicar ambos os lados da equação por um múltiplo de 10. Para descobrir qual será o múltiplo, devemos identificar quantos casas decimais devemos “andar” para que o período fique antes da vírgula. Dízima periódica composta multiplicar ambos os lados da equação por um múltiplo de 10, observando a quantidade de casas do antiperíodo. Depois repetir o mesmo processo da dízima periódica simples.
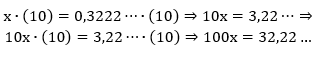
3º passo: Dízima periódica simples – diminuir a equação encontrada da equação inicial. Dízima periódica – diminuir a última equação encontrada da penúltima e isolar a incógnita.
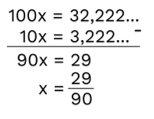
Vamos utilizar o método prático
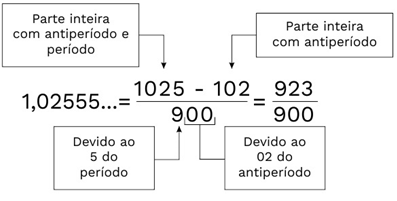
Exemplo 03. Determine a fração geratriz, usando o método prático, do número 1,02555…
01 . Expresse na forma de fração os seguintes números racionais
a) 0,777….
b) 1,3232….
c) 1,444….
d) 0,033…
e) 2,35111…
02 . (Enem 2015 – ADAPTADO) No contexto da matemática recreativa, utilizando diversos materiais didáticos para motivar seus alunos, uma professora organizou um jogo com um tipo de baralho modificado. No início do jogo, vira-se uma carta do baralho na mesa e cada jogador recebe em mãos nove cartas. Deseja-se formar pares de cartas, sendo a primeira carta a da mesa e a segunda, uma carta na mão do jogador, que tenha um valor equivalente àquele descrito na carta da mesa. O objetivo do jogo é verificar qual jogador consegue o maior número de pares. Iniciado o jogo, a carta virada na mesa e as cartas da mão de um jogador são como no esquema:
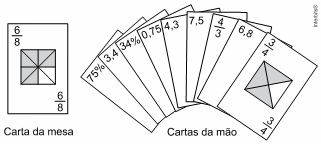
Segundo as regras do jogo, quantas cartas da mão desse jogador podem formar um par com a carta da mesa?


“Nas grandes batalhas da vida, o primeiro passo para a vitória é o desejo de vencer!” Mahatma Gandhi

Se for possível, você pode baixar ou imprimir a sua atividade.