Estudo dos métodos de contagem (Princípio Fundamental Da Contagem)

A parte da matemática que estuda o número de possibilidades de um evento ocorrer é denominada de Análise Combinatória. Em uma linguagem simplificada, a Análise Combinatória é a arte de contar. Nem sempre contar é um processo simples. Porém, na maioria das vezes só teremos que contar essas possibilidades. A técnica que permite a descrição das possibilidades de um experimento é chamada de Diagrama ou Árvore de Possibilidades.

Árvore ou Diagrama de possibilidades

É um esquema que nos permite a visualização de todas as possibilidades de um acontecimento, a partir de um diagrama que se ramifica de acordo com as possibilidades do evento considerado. Para melhor explicar esta técnica vamos nos apoiar em um exemplo.

Exemplo 01. Uma moeda é lançada 3 vezes. Qual é o número de sequências possíveis para cara ou coroa?

Solução: Note que no primeiro lançamento existem duas possibilidades: pode sair cara (K) ou pode sair coroa (C);

Já no segundo lançamento, existem quatro sequências possíveis. São essas: {(K,K);(K,C);(C,K);(C,C)};

Ao considerarmos o terceiro lançamento, existem agora oito sequências possíveis, que são: {(K,K,K); (K,K,C); (K,C,K); (K,C,C); (C,K,K); (C,K,C); (C,C,K); (C,C,C)}. Pelo diagrama teremos:

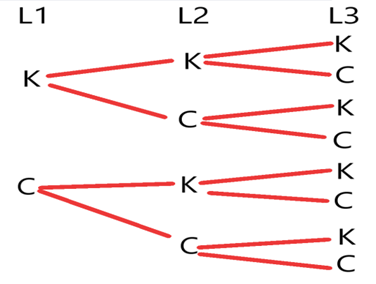
Fonte: O autor

Portanto temos oito sequências possíveis.

É importando notar que, se trocarmos a moeda por um dado com seis faces, e considerarmos os mesmos lançamentos teremos um número de possibilidades extremamente maior, pois para o primeiro lançamento teríamos seis possibilidades. No segundo lançamentos, para cada uma das seis primeiras ramificações, teríamos outras seis ramificações, e assim por diante, até o último lançamento.

Exemplo 02.  Para ir ao clube, Júnior deseja usar uma camiseta, uma bermuda e um par de tênis. Sabendo que ele dispõe de 4 camisetas, 2 bermudas e 3 pares de tênis, de quantas maneiras distintas poderá vestir-se?

Solução: Note que na primeira escolha Júnior dispunha de 4 camisetas {C1, C2, C3, C4}. Já na segunda escolha, da bermuda, dispunha de 2 possibilidades {B1, B2} e, para a terceira escolha, possui 3 pares de tênis {T1, T2, T3}, assim nosso diagrama será:

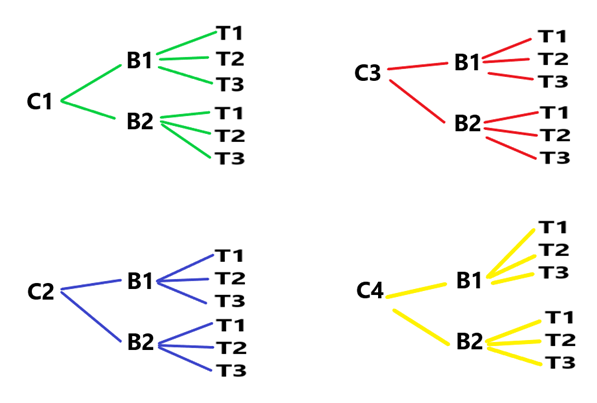
Fonte: O autor

Portanto, nestas condições, Júnior terá 24 possibilidades para se vestir.

Princípio Fundamental da Contagem

O princípio fundamental da contagem, também chamado de princípio multiplicativo, é utilizado para encontrar o número de possibilidades para um evento constituído de n etapas. Para isso, as etapas devem ser sucessivas e independentes.

Se a primeira etapa do evento possui  possibilidades e a segunda etapa é constituída de  possibilidades, então existem  possibilidades.

Portanto, o princípio fundamental da contagem é a multiplicação das possibilidades de cada etapa de um evento para determinar o total de possibilidades.

Se um acontecimento ocorrer em “n” etapas distintas e independentes entre si, A = {E₁, E₂, E₃, E₄, … ,E_n}, então o número total de possibilidades deste acontecimento ocorrer P(A) é obtido fazendo-se o produto entre o número de possibilidades de ocorrência de cada etapa, ou seja, é:

P(A) = P₁∙ P₂∙ P₃∙… ∙ P_n

Onde:

• P₁ é o número de possibilidades da 1ª etapa (E₁);
• P₂ é o número de possibilidades da 2ª etapa (E₂);
• P₃ é o número de possibilidades da 3ª etapa (E₃);
• Pn é o número de possibilidades da n-ésima etapa (E_n);

Vamos voltar à situação problema do exemplo 1:

Uma moeda é lançada 3 vezes. Qual o número de sequências possíveis para cara ou coroa?

Solução: Note que no primeiro lançamento existem duas possibilidades: pode sair cara (K) ou pode sair coroa (C). Sendo P(L) o número de possibilidades do lançamento, teremos, pelo Princípio Fundamental da Contagem:

Total de possibilidades = P(L1) x P(L2) x P(L3) = 2 x 2 x 2 = 8 possibilidades.

Note que por essa técnica, não existe a preocupação em descrever cada possibilidade, e sim só contamos o total de possibilidades.

Nestas condições, aplicando o mesmo critério, podemos contar quantas possibilidades de resultados podem ser obtidas se, ao invés de uma moeda, tivéssemos utilizado um dado. Assim teremos:

Total de possibilidades = P(L1) x P(L2) x P(L3) = 6 x 6 x 6 = 216 possibilidades.

Exemplo 3. Para ir ao clube, Júnior deseja usar uma camiseta, uma bermuda e um par de tênis. Sabendo que ele dispõe de 4 camisetas, 2 bermudas e 3 pares de tênis, de quantas maneiras distintas poderá vestir-se?

Solução: Número de possibilidades para se vestir P(V) depende do número de possibilidades de cada etapa:

1ª Etapa: Escolha da camiseta P(C) = 4;

     2ª Etapa Escolha da bermuda P(B)= 2;

    3ª Etapa Escolha do tênis P(T)= 3,

P(V) = P(C) ∙ P(B) ∙ P(T) = 4 ∙ 2 ∙ 3 = 24 possibilidades.

Nestas condições, Júnior possui 24 maneiras distintas para se vestir.

Exemplo 4. As atuais placas de licenciamento de automóveis constam de sete símbolos (caracteres) sendo três letras, dentre as 26 do alfabeto, seguidas de quatro algarismos. Quantas placas distintas podem ter sem a repetição de letras ou de algarismos, ou seja, com todos os caracteres distintos?

Solução: Neste caso perceba que cada caractere da placa possui uma quantidade de escolhas possíveis.

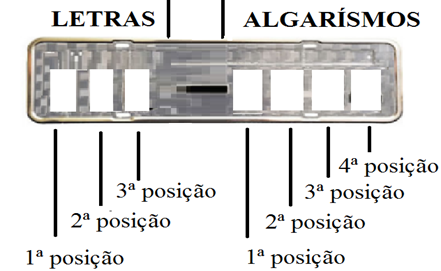
Fonte: O autor

Para a 1ª letra: 26 possibilidades de escolha;

Para a 2ª letra: 25 possibilidades de escolha, uma vez que uma letra já foi escolhida;

Para a 3ª letra: 24 possibilidades de escolha, pois agora, duas letras já foram escolhidas.

Para o 1º algarismo: 10 possibilidades de escolha.

Para o 2º algarismo: 9 possibilidades de escolha, pois um algarismo já foi usado;

Para o 3º algarismo: 8 possibilidades de escolha, pois dois algarismos já foram usados;

Para o 4º algarismo: 7 possibilidades de escolha, pois três algarismos já foram usados.

Portanto, pelo Princípio Fundamental da Contagem:

N^o de Placas = 26 x 25 x 24 x 10 x 9 x 8 x 7 = 78.624.000 placas possíveis.

Nestas condições, o número de placas possíveis é 78.624.000.

      Outros problemas de contagem

      Anagramas: são permutaçoes (trocas) das letras de uma palavra, formado novas palavras, com ou sem sentido.

Exemplo 5. Quantos anagramas possuem a palavra ANEL?

Solução: A palavra ANEL tem 4 letras e qualquer uma destas letras pode assumir a primeira posição na palavra.                          

Escolhendo esta letra, sobram outras 3 letras para a segunda posição. Em seguida, há 2 letras disponíveis e, escolhida essa 3^a letra, restará apenas 1 opção para 4^a letra.

Veja:

Assim, temos 24 anagramas da palavra ANEL.