AULA 15/2022 – Sequências recursivas e não recursivas - 29/08/2022
Sequências numéricas
Sequência numérica é uma sucessão de números que geralmente possui uma lei de formação, com especificidades, como por exemplo, a sequência de números pares. Nas sequências numéricas é importante descobrir regularidades, para determinar os termos que faltam, ou os termos futuros.
Uma sequência numérica deve ser representada entre parênteses e ordenada. Exemplos:
- Sequência dos números naturais: (0; 1; 2; 3; 4; 5; 6; …)
- Sequência dos números primos positivos: (2; 3; 5; 7; 11; 13; 17; 19; …)
- Sequência dos números ímpares positivos: (1; 3; 5; 7; 9; …):
- Sequência dos múltiplos de 3: (0; 3; 6; 9; 12; 15; 18; …)
As sequências são classificadas em: finita ou infinita. Em uma sequência numérica, o primeiro termo é representado por a1, o segundo termo por a2, o terceiro termo por a3, e assim sucessivamente. Em uma sequência numérica finita o último termo é representado por an. A letra n indica a quantidade de termos da sequência ou a posição de cada termo. ( n ∈ N)
Situação Problema
Em 1202, um matemático italiano conhecido como Fibonacci propôs o seguinte problema:
“Um homem pôs um par de coelhos num lugar cercado por todos os lados por um muro. Quantos pares de coelhos podem ser gerados a partir desse par em um ano se, supostamente, todos os meses cada par dá à luz um novo par, que é fértil a partir do segundo mês?”
O problema afirma que
- No primeiro mês nasce apenas um casal;
- Casais amadurecem e reproduzem-se apenas após o segundo mês de vida;
- Não há problemas genéticos no cruzamento consanguíneo;
- Todos os meses, cada casal fértil dá à luz um novo casal;
- Os coelhos nunca morrem.
Dessa forma, temos:
Mês 0 – Existe apenas um par de coelhos.
Mês 1 – Os coelhos só acasalam ao segundo mês, logo continua a haver apenas um casal.
Mês 2 – Neste mês já a fêmea deu à luz um par de coelhos, existindo agora dois pares de coelhos.
Mês 4 – O par original tem mais um par de coelhos. O par nascido no mês 2 também dá à luz e o par nascido no mês 3 acasalam, mas ainda não dão à luz. Isto faz um total de cinco pares.
Mês 5 – Todos os pares que nasceram até há dois meses dão à luz, fazendo na totalidade 5 pares.
Observe o fluxograma:
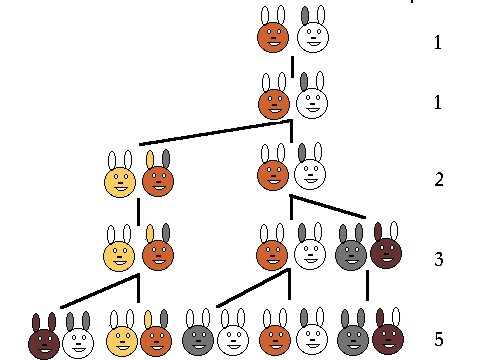
Ou seja:
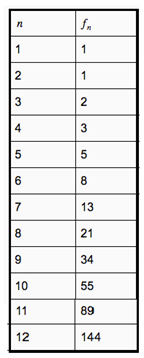
Assim, com base na tabela, conseguimos resolver o problema, pois sabemos que o número de casais cresce de acordo com os termos da sequência, ou seja, o número de pares de coelhos em determinado mês, é a soma dos pares de coelhos existentes nos dois meses anteriores a este.
Então, ao final de um ano (12 meses) teremos: f12 =144 casais de coelhos.
Desta forma, o problema acima é conhecido como Sequência de Fibonacci e é uma sequência recursiva considerada a mais antiga da Europa.
Sequência recursiva
Uma sequência é recursiva quando um termo depende dos termos anteriores.
Exemplo 1
Quantos cubos formarão a próxima figura e como chegar à resposta?
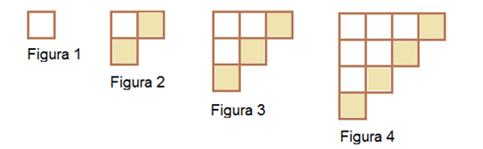
Representação numérica:
Figura 1 = 1
Figura 2 = 3
Figura 3 = 6
Figura 4 = 10
- Nesse sentido, quantos cubos teria a figura 5?
Perceba que o número de quadrados aumenta de acordo com a sequência dos números naturais, oberve
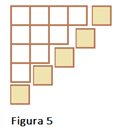
Figura 1 = 0 + 1
Figura 2 = 1 + 2 à (Número de cubos da figura 1) + 2 = 3
Figura 3 = 3 + 3 à (Número de cubos da figura 2) + 3 = 6
Figura 4 = 6 + 4 à (Número de cubos da figura 3) + 4 = 10
Figura 5 =10 +5 à (Número de cubos da figura 4) + 5 = 15
- Logo a figura 5 possui 15 quadradinhos.
Dessa forma, podemos representar essa sequência recursiva de outras formas:

Logo, a figura 15, seguindo essa sequência, teria 15 quadradinhos.
Outra forma de representarmos uma sequência é por meio de um fluxograma, que ao invés de mostrar uma lei de formação expressa no formato de fórmula, indica cada passo da formação de uma sequência.
Exemplo 2 Qual a sequência apresentada no fluxograma abaixo?
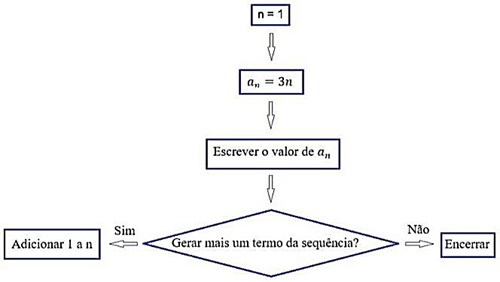
Perceba que:
Para n = 1, an = 3
Para n = 1 + 1 (Pois para gerar o próximo termo temos que adicionar 1 ao n) , an = 6.
Para n = 2 + 1 (Pois para gerar o próximo termo temos que adicionar 1 ao n) , an = 9.
Para n = 3 + 1 (Pois para gerar o próximo termo temos que adicionar 1 ao n) , an = 12.
Logo, baseado na lei de formação e no fluxograma, temos que a sequencia apresentada representa os multiplos não nulos de 3.
Exemplo 3
Quais são os 5 primeiros termos dessa sequência?
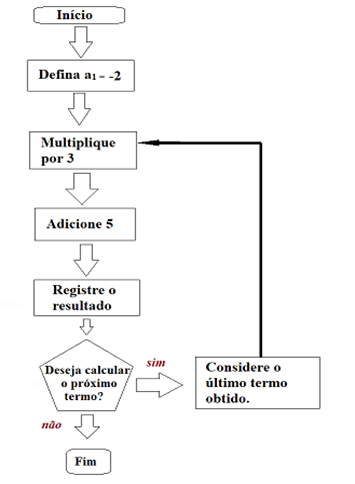
Para conseguirmos responder a esse questionamento, basta seguirmos o fluxograma, ou seja:
O primeiro termo dessa sequência é dado = -2
O segundo termo será: -2 · 3 + 5 = -6 + 5 = -1
O terceiro termo dessa sequência será:
-1 · 3 + 5 = -3 + 5 = 2
O quarto termo dessa sequência será:
2 · 3 + 5 = 6 + 5 = 11
O quinto termo dessa sequência será:
11 · 3 + 5 = 33 + 5 = 38
Assim, os cinco primeiros termos da sequência apresentada pelo fluxograma são -2, -1, 2, 11 e 38.
Sequências não recursivas
As sequências não recursivas são aquelas que não dependem de termos anteriores para que se determine o próximo termo. Pode-se obter o valor de um elemento da sequência apenas pela sua posição. Por exemplo:
(6,12,18,24…)
Não é necessário saber o último termo para determinar o seguinte. Observando atentamente, essa sequência é formada pelos múltiplos de 6.
Exemplo 4

O segmento verde mede 3 cm, o segmento azul mede o dobro disso e o segmento vermelho o triplo do verde. É uma sequência porque segue uma regularidade.
Representação numérica: (3; 6; 9; 12; 15; …).

Estamos vendo então, que uma sequência numérica possui um padrão e pode ser representada por uma expressão algébrica.
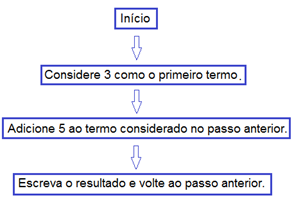
Exemplo 5
Observe a sequência numérica a seguir:
1024; 512; 256; 128; …
- Qual será o próximo valor desta sequência? Qual é o padrão?
O próximo termo será = 64 (128 : 2 = 64), pois o padrão apresentado nesta sequência é o valor anterior dividido por 2.

Observem como utilizar um fluxograma para esta sequência:
ATIVIDADES
1. Escreva os próximos três termos de cada sequência.
a) (0; 5; 10; 15; 20; ____; ____; ____; … )
b) (31; 27; 23; 19; 15; ____; ____; ____; … )
2. A sequência a seguir apresenta os sete primeiros números primos: 2, 3, 5, 7, 11, 13, 17, …
a) Escreva os três próximos termos dessa sequência.
_______________________________________________________________________________________
b) Classifique essa sequência em recursiva ou não recursiva. Justifique sua resposta.
_______________________________________________________________________________________
3. Observe a sequência a seguir.

a) Quantos losangos devem compor as duas próximas figuras mantendo o padrão dessa sequência?
_______________________________________________________________________________________
b) Elabore um quadro que relacione a posição da figura e o número de losango que a compõe.
______________________________________________________________________________________
c) Quantos losango devem conter as figuras que ocupam as posições 10 e 11?
______________________________________________________________________________________
d) Qual é a expressão algébrica que descreve o padrão dessa sequência?
______________________________________________________________________________________
4. Complete as sequencias numéricas abaixo, e seus respectivos fluxogramas.
a) 1, 5, 10, 15, 20, _______, _______, _______, …

b) 31, 27, 23, 19, 15, _______, _______, _______, …

5. A sequência formada pelas potências de 3 é um exemplo de sequência recursiva. Observe os três primeiros termos dessa sequência: 0,1, 3, 9, …
Elabore um fluxograma que represente uma maneira de obter todos os termos dessa sequência.
Lembre-se que: Fluxograma: é um tipo de diagrama, ou seja, uma representação esquemática de um processo ou algoritmo
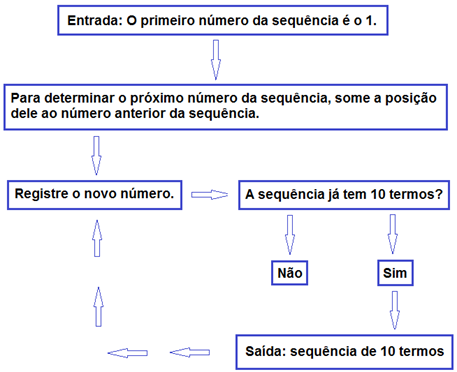
6. Construa a sequência numérica descrita pelo fluxograma seguinte:
7. Observe a sequência de peças de dominó a seguir.
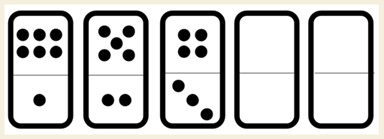
Quantas bolinhas aparecerão nas peças seguintes? Complete o desenho e faça uma análise de seus resultados.
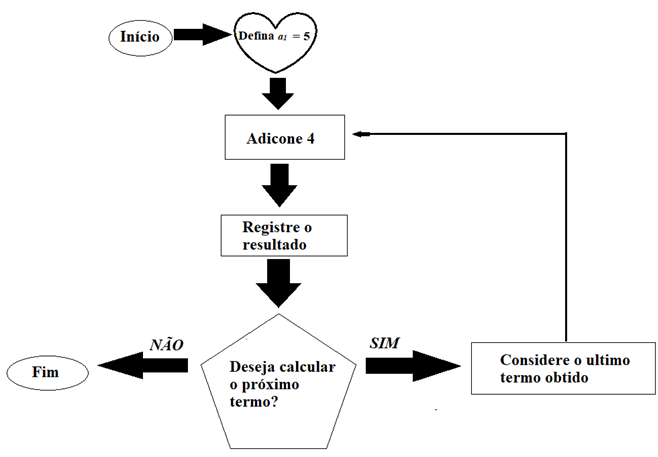
8. Observe o fluxograma abaixo e determine os 10 primeiros termos da sequência por ele descrita.
9. As figuras representam caixas numeradas de 1 a n, contendo bolinhas. A quantidade de bolinhas em cada caixa varia de acordo com o número dessa caixa.
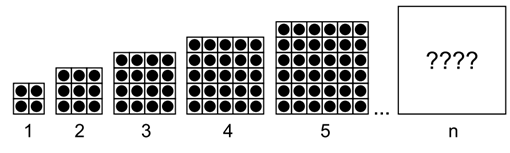
Determine a quantidade de bolinhas da figura 10.
10. Enumere cada sequência numérica na coluna da direita de acordo com as respectivas expressões que as representam na coluna da esquerda.
