AULA 19/2022 – Representação de números racionais - 26/10/2022
O CONJUNTO DOS NÚMEROS RACIONAIS
Os números racionais são aqueles que podem ser escritos na forma de fração, em que o numerador é um número inteiro e o denominador é um número inteiro não nulo (diferente de zero). Observe como podemos descrever esse conjunto utilizando a linguagem matemática.

Diferentes escritas de um número racional:
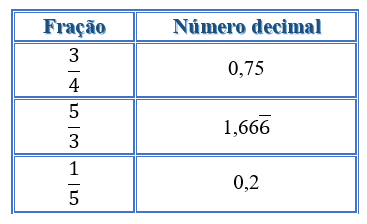
NÚMEROS DECIMAIS
Os números decimais são números racionais (Q) não inteiros expressos por vírgulas, que possuem casas decimais e podem ser positivos ou negativos. Analisando o número 5,1561 temos:
5 → Parte inteira
1 → Décimos
5 → Centésimos
6 → Milésimos
1 → Décimo de Milésimos
Veja que os algarismos 5 e 1 aparecem duas vezes no número, entretanto, eles representam quantidades diferentes. O 5 (parte inteira) indica 5 unidades, enquanto os números que estão à direita da vírgula representam frações de um inteiro. A leitura do número deve ser feita da seguinte maneira: Cinco inteiros, mil quinhentos e sessenta e um décimos de milésimos.
Número decimal exato e dízima periódica

Dízima periódica

Na representação decimal a dízima periódica pode ser representada de duas maneiras.Podemos inserir, ao final do número, reticências (…) ou podemos colocar um traço acima do seu período (parte que se repete na dízima).
Exemplos:

Como as dízimas periódicas pertencem ao conjunto dos números racionais, elas podem ser representadas como uma fração que denominamos fração geratriz. Lembre-se que, nos casos em que temos dízimas exatas, podemos obtê-las a partir das frações em que o denominador possui base 10.

DÍZIMA PERIÓDICA E FRAÇÃO GERATRIZ.
O número 0,333… é chamado de decimal periódico não exato (dízima periódica), e sendo um número racional, podemos associá-lo a uma fração, denominada de fração geratriz. Logo, toda dízima periódica, deve possuir uma forma fracionária.
Como temos dois tipos de dízimas periódicas, encontramos as respectivas frações geratriz, de duas maneiras distintas:
Dízima periódica simples:
1º passo: Igualar a dízima periódica a uma incógnita, por exemplo x, de forma a escrever uma equação do 1º grau com uma incógnita.
2º passo: Multiplicar ambos os lados da equação por um múltiplo de 10. Para descobrir qual será o múltiplo, devemos identificar quantos casas decimais devemos “andar” para que o período fique antes da vírgula.
3º passo: Subtrair da equação encontrada, a equação inicial.
4º passo: Resolver a equação obtida no 3º passo.

Seguindo os passos, temos:
1º passo: Igualar a dízima periódica a uma incógnita de forma a escrever uma equação do 1º grau:
2º passo: Multiplicar ambos os lados da equação por um múltiplo de 10. Para descobrir qual será o múltiplo, devemos identificar quantos casas decimais devemos “andar” para que o período fique antes da vírgula.
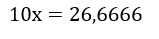
3º passo: Subtrair da equação encontrada, a equação inicial, isto é,

MÉTODO PRÁTICO
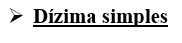
Devemos colocar:
No numerador, um número formado pelos algarismos inteiros e o período, menos os algarismos inteiros, sem a vírgula.
No denominador, um número formado apenas por algarismos iguais a nove. A quantidade de “noves” dependerá de quantos algarismos formam o período da dízima.
Exemplo. Determine a fração geratriz do número 6,454545…
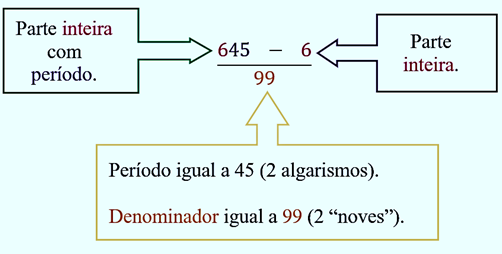
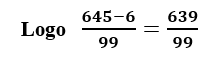
Dízima periódica composta:
1º passo: Igualar a dízima periódica a uma incógnita, de forma a escrever uma equação do 1º grau com uma incógnita.
2º passo: Multiplicar ambos os lados da equação por um múltiplo de 10, observando a quantidade de casas do antiperíodo. Depois repetir o mesmo processo da dízima periódica simples.
3º passo: Subtrair da última equação encontrada, a penúltima equação.
4º passo: Resolver a equação obtida no 3º passo.

Seguindo os passos, temos:
1º passo: Igualar a dízima periódica a uma incógnita, de forma a escrever uma equação do 1º grau.
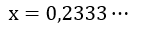
2º passo: Multiplicar ambos os lados da equação por um múltiplo de 10, de modo que o antiperíodo fique antes da vírgula. Depois, obter outra equação, multiplicando por um múltiplo de 10 também, de modo que o antiperíodo e o período fiquem antes da vírgula.
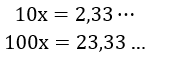
3º passo: Subtrair da última equação encontrada, a penúltima equação.
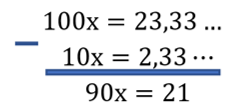
4º passo: Resolver a equação obtida no 3º passo.
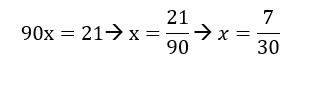
MÉTODO PRÁTICO
Devemos colocar:
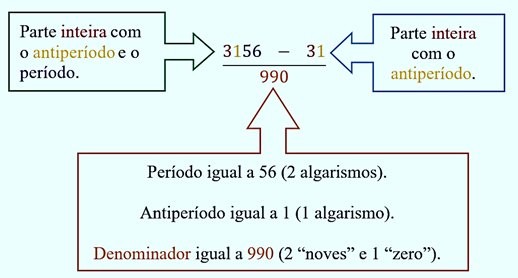
No numerador uma subtração entre o número formado pelos algarismos da parte inteira, o antiperíodo e o período (sem a vírgula) e o número formado pela parte inteira e o antiperíodo, também sem a vírgula.
No denominador, um número formado apenas por algarismos iguais a nove. A quantidade de “noves” dependerá de quantos algarismos formam o período da dízima. A quantidade de “zeros” dependerá de quantos algarismos formam o antiperíodo.
Exemplo: Determine a fração geratriz da dízima
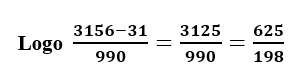
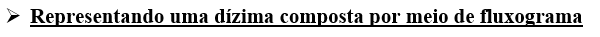
ATIVIDADES
1. Dada a fração, diga que número decimal ela representa:

2. Dê dois exemplos de dízima periódica simples e composta.
3. Expresse na forma de fração os seguintes números racionais
A) 0,777….
B) 1,3232….
C) 1,444….
D) 0,033…
E) 2,35111…
F) 0,888…
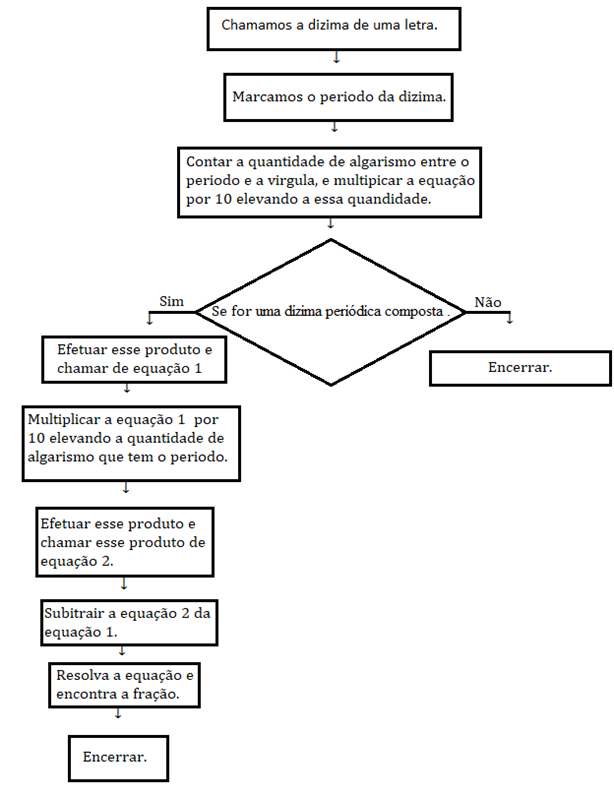
4. Analise os números a seguir:
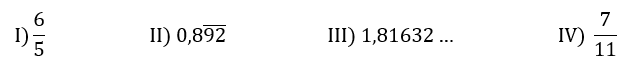
Podemos escrever como uma dízima periódica:
A) somente I e II.
B) somente II e III.
C) somente II e IV.
D) somente III e IV
5. Sobre as dízimas, julgue as afirmativas a seguir:
I. Toda dízima periódica é um número racional.
II. Tantos as dízimas periódicas, quanto as não periódicas possuem fração geratriz.
III. Chamamos de fração geratriz a representação fracionária da dízima periódica.
Assinale a alternativa correta:
A) Somente a afirmativa I é verdadeira.
B) Somente as afirmativas I e II são verdadeiras.
C) Somente as afirmativas III é verdadeira.
D) Somente a afirmativa II é falsa
6. Com base no conteúdo estudado sobre dízimas periódicas, julgue as afirmativas a seguir:
I. A representação decimal da fração é uma dízima periódica.
II. Uma dízima periódica pode ser um número racional ou irracional.
III. Uma dízima periódica composta possui parte inteira, parte não periódica e período.
Marque a alternativa correta:
A) Somente a afirmativa III é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa I é verdadeira.
D) Somente a afirmativa II e III são verdadeiras.
7. Ao realizar uma divisão encontrei como resultado o número . Com base nesse resultado, julgue as afirmativas a seguir:
I. O resultado é um número racional.
II. O resultado é uma dízima periódica composta.
III. O resultado não pode ser representado como uma fração.
Marque a alternativa correta:
A) Somente a afirmativa I e II são verdadeiras.
B) Somente a afirmativa II e III são verdadeiras.
C) Somente a afirmativa I e III são verdadeiras.
D) Todas as afirmativas são verdadeiras.
8. Complete a tabela com as representações fracionárias, decimais dos seguintes números racionais:
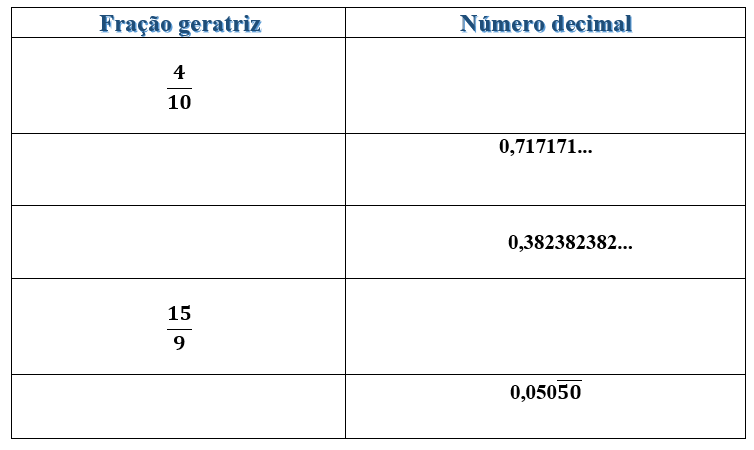
9. Considere os números na tabela a seguir classifique-os em dizimas periódicas simples e dízimas periódicas compostas.

10. Considere as frações geratrizes a seguir e obtenha as dízimas periódicas, especifique se é uma dízima periódica simples ou composta e escreva o período e o antiperíodo (quando existir).
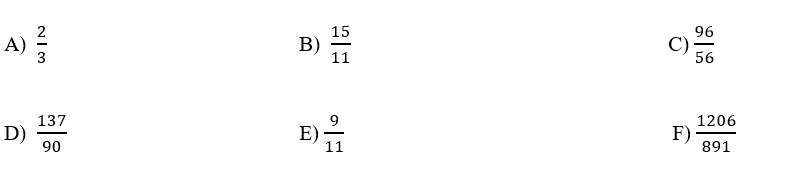
11. O número real representado por 12,3 … é

12. Apresente o resultado das expressões abaixo na forma fracionária:
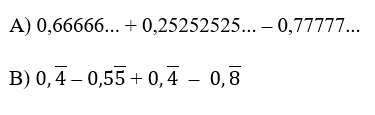
13. Se x = 0,949494… e y = 0,060606…, então x + y é igual a

14. Considere que a = e b = , escreva o resultado de
A) a · b
B) a + b
C) a – b
D) a ÷ b

16. Sejam x = 1 e y = 0,9999… Quais das afirmações a seguir são verdadeiras?
A) x < y
B) x < y
C) x = y
D) x + y =
17. Eloisa dividiu dois números inteiros positivos em sua calculadora e obteve como resultado a dízima periódica 1,929292… Se a divisão tivesse sido feita na outra ordem, ou seja, o menor dos dois números dividido pelo maior deles, o resultado obtido por Eloisa na calculadora teria sido?
18. João dividiu dois números inteiros positivos e obteve como resultado a dízima periódica 0,1777… Se ao invés de dividir ele tivesse multiplicado os dois números, o resultado obtido por João teria sido?