OLÁ! VAMOS INICIAR NOSSA ATIVIDADE!

Construção de figuras planas semelhantes

1. Na malha quadriculada

         Quando falamos em ampliação de uma imagem, consideramos que as medidas de abertura dos ângulos dessa imagem são mantidas e que as medidas de comprimento de suas dimensões são multiplicadas por um mesmo número maior que 1. Do mesmo modo na redução de uma imagem, neste caso as medidas são divididas por um mesmo número maior que 1.

Exemplo:

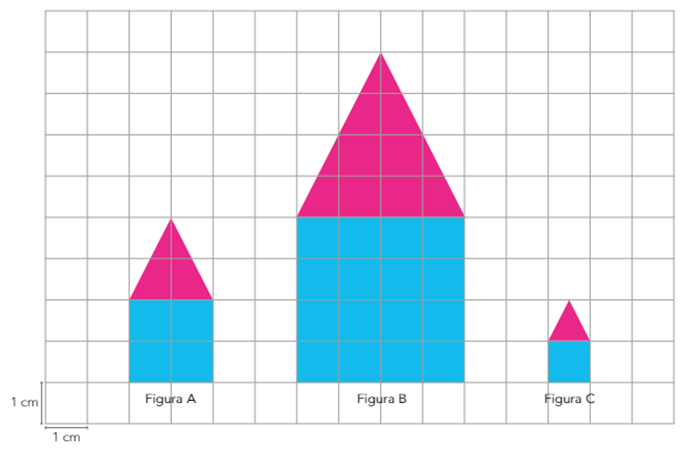
        Com base na malha quadriculada, nas medidas das aberturas dos ângulos das três figuras e nas medidas de comprimento dos lados delas, podemos afirmar, em relação à figura A, que a figura B é uma ampliação e que a figura C é uma redução dela.

2. No plano cartesiano

             Além da malha quadriculada, podemos ampliar ou reduzir uma figura utilizando o plano cartesiano.

Exemplo:

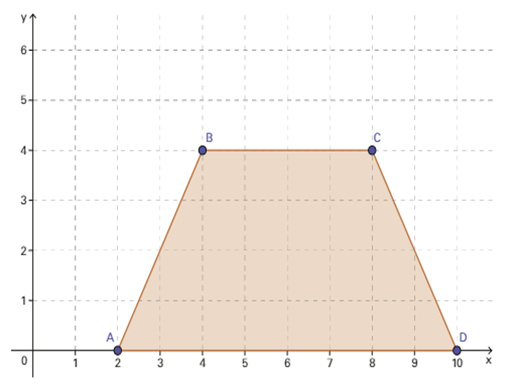
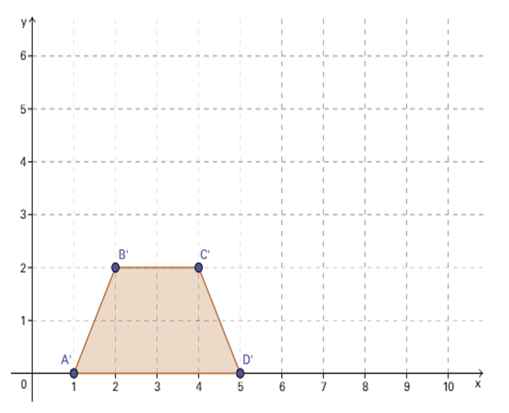
            Observe que os pares ordenados dos quatro vértices do trapézio ABCD são: A(2, 0), B(4, 4), C(8, 4), D(10, 0). Ao dividir essas coordenadas por 2, obtemos os seguintes pares ordenados: A’(1, 0), B’(2, 2), C’(4, 2), D’(5, 0). Ligando esses pontos no plano cartesiano, obtemos o novo trapézio A’B’C’D’.

Atividades

1. Qual das figuras a seguir é uma ampliação da figura O?

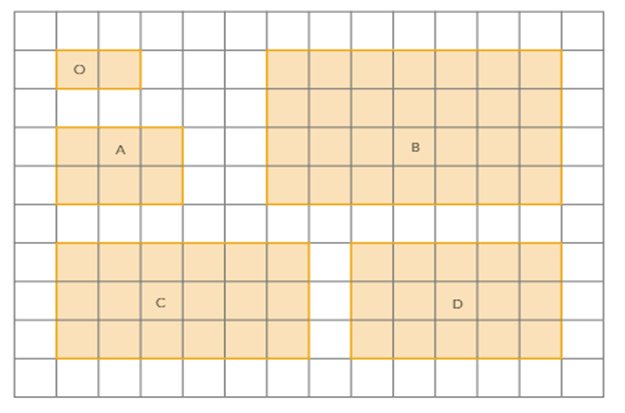
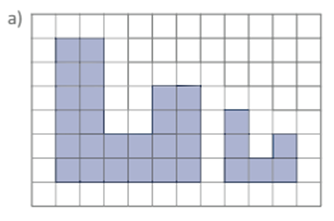
2. Construa uma redução da figura a seguir na mesma malha quadriculada.

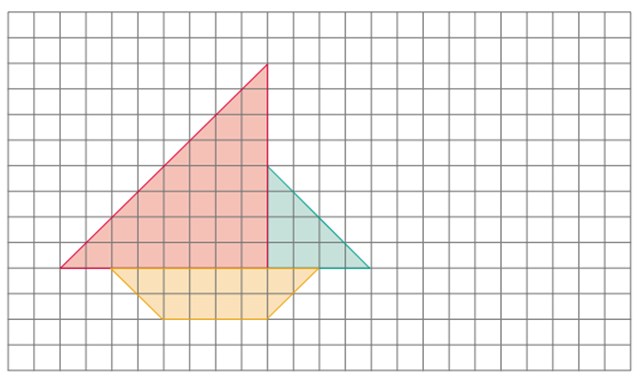
3. Verifique se as figuras de cada item a seguir são semelhantes. Em caso afirmativo, indique se as medidas de comprimento dos lados foram multiplicadas ou divididas da primeira para a segunda figura. Verifique também por qual número elas foram divididas ou multiplicadas.

4. Observe o quadrilátero no plano cartesiano a seguir e, então, faça o que se pede:

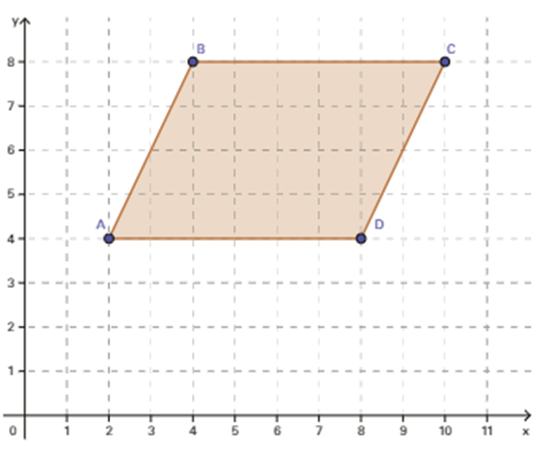
a) Como pode ser classificado esse quadrilátero?

b) Determine os pares ordenados de seus vértices.

c) Construa uma redução desse quadrilátero no plano cartesiano a seguir de modo que a medida de cada um de seus lados seja a metade da medida dos lados correspondentes do quadrilátero original.

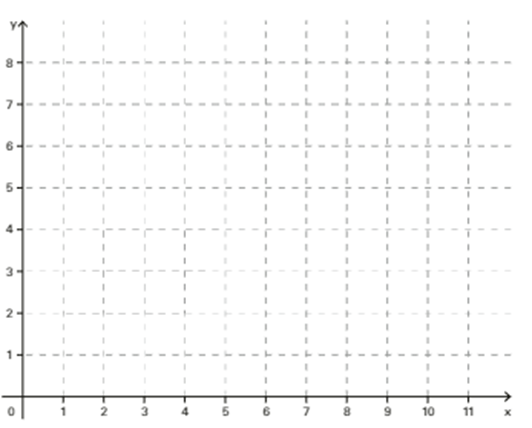
5. O perímetro de um quadrado é 48 cm. Uma redução desse quadrado tem lados cujas medidas de comprimento são  das medidas de comprimento dos lados do quadrado original. Determine o perímetro desse quadrado reduzido.

6. Na figura a seguir há um quadrado dividido em 2 quadrados com áreas diferentes e 2 retângulos congruentes. O quadrado menor tem área igual a 9 cm², e a área do segundo maior quadrado é 64 cm². Determine a medida de comprimento do lado do quadrado maior, o seu perímetro e a sua área.

7. (Prova Brasil) Os desenhos a seguir representam o formato de um jardim que será construído em uma praça da cidade. Inicialmente pensou-se num jardim pequeno, mas, devido ao grande entusiasmo que causou na população da cidade, o prefeito solicitou que fizessem um novo projeto, com desenho maior. O novo projeto terá área:

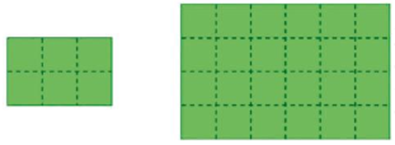
a) (  ) 2 vezes maior que o primeiro.

b) (  ) 3 vezes maior que o primeiro.

c) (  ) 4 vezes maior que o primeiro.

d) (  ) 6 vezes maior que o primeiro.

8. Marco entregou uma folha de papel quadrada de 25 cm² de área para Gabriel e pediu a ele que confeccionasse em outra folha um quadrado com o dobro da medida de comprimento do lado da folha que recebeu. Quanto deverá se a área do quadrado de Gabriel?

a) (  ) 25 cm²

b) (  ) 50 cm²

c) (  ) 75 cm²

d) (  ) 100 cm²

MUITO BOM! CONCLUÍMOS…VAMOS REVISAR!!!

     Baixe e imprima sua atividade!