Equações do 1º Grau – Atividade 7 - 20/04/2021
EQUAÇÕES DO PRIMEIRO GRAU
Definição: Chama-se equação do 1º grau toda equação da forma, ou redutível à forma:
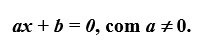
Nesta equação a e b são chamados de coeficientes e x recebe o nome de incógnita. A parte que fica antes da igualdade (do lado esquerdo) é chamada de 1º membro, a parte que fica depois da igualdade (à direita da igualdade) é denominada de 2º membro. Na equação do 1º grau a incógnita é o valor que se deseja determinar.
Exemplo 1:
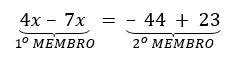
Resolver uma equação significa determinar o valor que atribuído a x fará com que a igualdade se torne verdadeira, e será chamado de raiz da equação.
Para isso temos com método de resolução a aplicação dos seguintes princípios algébricos:
PRINCÍPIO ADITIVO: Quando se soma (ou se subtrai) qualquer número real nos dois membros de uma equação, ela não se altera.
PRINCÍPIO MULTIPLICATIVO: Quando se multiplica (ou se divide) toda uma equação por qualquer número real diferente se zero, ela não se altera.
A aplicação desses princípios garante a obtenção de equações equivalentes, que são assim denominadas por possuírem o mesmo conjunto solução.
Quando juntamos os dois princípios acima formamos o chamado Princípio da Igualdade.
PRINCÍPIO DA IGUALDADE: Uma equação não se altera quando adicionamos, subtraímos, multiplicamos ou dividimos um mesmo número (diferente de zero) a cada um de seus membros.
MÉTODO DE RESOLUÇÃO
Com base na aplicação dos princípios citados acima, temos o desenvolvimento dos seguintes passos:
1º) Coloca-se todos os coeficientes que estiverem acompanhados pelas incógnitas em um dos membros da igualdade e aqueles que não estão acompanhados do outro.
Então teremos:
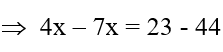
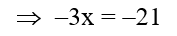
3º) Divide-se toda equação de modo a deixar o coeficiente de x igual a 1. Neste caso divide-se toda equação por ( –3 )
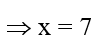
Logo o conjunto verdade (V) ou conjunto solução (S) é {7}.
O conjunto verdade ou conjunto solução é o conjunto das raízes da equação.
Exemplo 2) Resolva a equação do 1º grau.
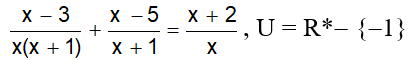
Observe que existe uma condição para restringir os valores que x poderá assumir.
U = R*- {-1}
Por esta, x só poderá assumir valores que sejam diferentes de 0 e de -1. Isso deve-se ao fato de que se x assumir qualquer desses valores o resultado do denominador será zero o que não é possível, uma vez que não existe divisão por zero.
Esta condição é chamada de Condição de Domínio ou Condição de Existência.
MÉTODO DE RESOLUÇÃO
Neste caso o primeiro passo a ser dado é tirarmos o mínimo múltiplo comum dos denominadores nos dois membros da equação, a fim de reduzi-las ao mesmo denominador.
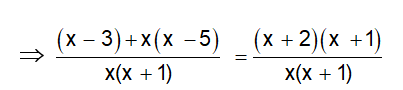
Agora que os denominadores dos dois membros são iguais pode-se simplificá-los
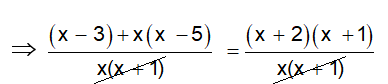
A equação restante será formada pelos denominadores dos dois membros.
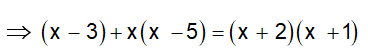
Em seguida, efetuam-se as operações algébricas indicadas nos dois lados da igualdade
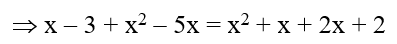
Daqui por diante, segue os mesmos passos do exemplo 1.

ATIVIDADES – PARTE I
01. Resolva as seguintes equações na variável x, sendo U = R:
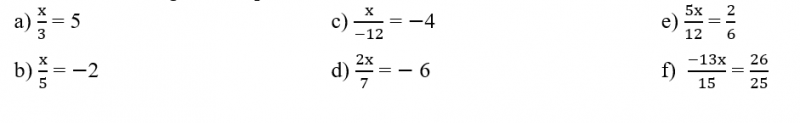
02. Resolva as seguintes equações na variável x, sendo U = R:
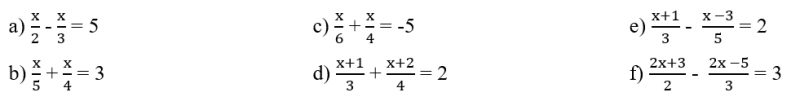
03) Utilizando a linguagem matemática para um número “x” real, escreva:
a) sucessor de um número:
b) o dobro de um número:
c) o triplo de um número:
d) o dobro do sucessor de um número:
e) a metade de um número:
f) a terça parte de um número:
g) quatro quintos de um número:
h) cinco quantos de o antecessor de um número:
04) Resolva os problemas atribuindo “x” à incógnita:
a) O dobro de um número somado a 7 é igual a 17 unidades. Qual é o número?
b) A terça parte do antecessor de um número subtraída de 15 resulta em 8 unidades. Que número é esse?
c) A soma do sucessor de um número com sua metade é igual a 16. Qual é o valor desse número?
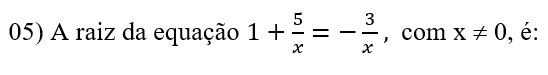
A) ( ) -2
B) ( ) +2
C) ( ) -8
D) ( ) +8
06. É de entendimento comum em matemática que o conjunto solução de uma equação o conjunto de todos os números reais, ou seja, em uma equação o valor que x poderá assumir é qualquer número real “ℝ”. No caso de uma equação fracionária devemos excluir todos os possíveis valores de x que possam zerar os denominadores das frações, uma vez que não existe divisão por zero.
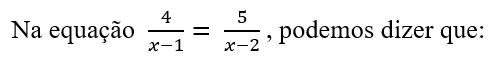
A) ( ) U = R – {1}.
B) ( ) U = R – {2}.
C) ( ) U = R – {1, 2}.
D) ( ) U = R* – {1, 2}.
07) Na distribuição de uma refeição em uma escola da rede estadual foram divididos igualmente para cada alunos para os 30 alunos de uma turma do 8º ano, 120 unidades de frutas entre peras e maçãs. Sabendo que cada aluno recebeu uma pera e x maçãs, podemos representar esta situação matemática por meio da equação

A) ( ) 1 maçã.
B) ( ) 2 maçãs.
C) ( ) 3 maçãs.
D) ( ) 4 maçãs.
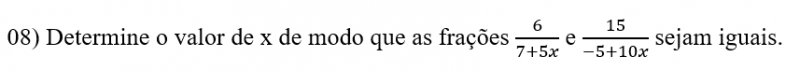
EQUAÇÃO LITERAL
Uma equação do primeiro grau na incógnita ‘x’ é dita literal se, além da incógnita x, aparecerem outras letras. Essas letras são chamadas de parâmetros. Resolver uma equação do 1º grau literal é ainda isolar o valor de x, contudo neste caso, a incógnita x ficará em função dos valores associados na equação se estes não se eliminarem no processo de resolução.
ATIVIDADES- PARTE II
09) Resolvas as seguintes equações literais na variável x, sendo U = R:
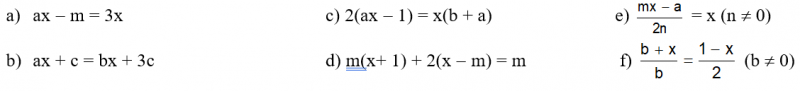
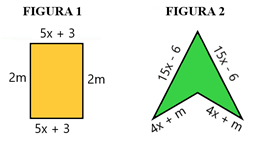
10) Determine os valores de x para os quais a figura 1 tem o mesmo perímetro da figura 2.
EQUAÇÕES DO 1º GRAU COM DUAS INCÓGNITAS.
Uma equação do 1º grau com duas incógnitas pode ser representada por uma sentença algébrica do tipo ax + by = c, em que a e b são coeficientes, c é o termo independente, pois não está sendo multiplicado por incógnitas e, x e y são as incógnitas. Veja os exemplos;
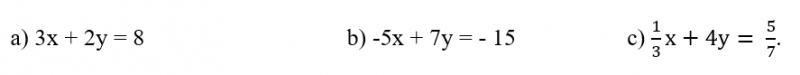
O conjunto de valores que atribuídos a ‘x’ e a ‘y’ satisfazem a igualdade é o conjunto solução que, neste caso, é representado pelo par ordenado (x, y). Observe a equação 3x + 2y = 8 admite como solução;
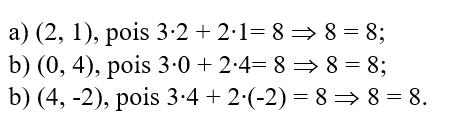
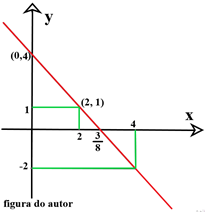
Percebemos então que existem uma infinidade de pontos que podem satisfazer a igualdade e, consequentemente, podemos representar o conjunto de todos os pontos que são solução da equação no plano cartesiano por meio de uma reta. Neste caso teremos a situação ilustrada ao lado.
É correto concluirmos que todos os pontos desta reta formam pares ordenados que são soluções da equação 3x + 2y = 8.
ATIVIDADES- PARTE III
11) Verifique para quais das equações abaixo o par ordenado (–1, 2) é solução:
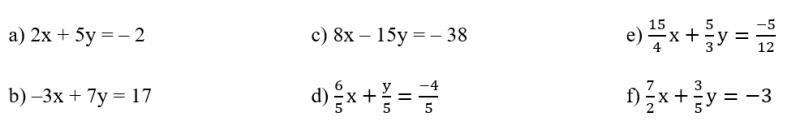
12) Resolva os problemas abaixo por meio de equações do 1º grau com duas incógnitas:
a) A soma de dois números é 57. O maior deles é igual ao menor, mais 5. Quais são os dois números?
b) Quero repartir 120 em duas parcelas. A maior delas deve superar a menor em 16 unidades. Quais devem ser as parcelas?
