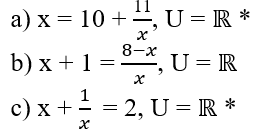Equações do 2º Grau e suas aplicações.Equações do 2º Grau e suas aplicações – Atividade 7 - 20/04/2021
EQUAÇÕES POLINOMIAIS DO 2º GRAU
Chama-se Equação Geral do 2º grau, toda equação do tipo ou redutível ao tipo ax2 + bx + c = 0, com a ¹ 0.
Em que:
- a, b e c são os coeficientes;
- a recebe o nome de coeficiente dominante;
- c recebe o nome de termo independente;
- x é a incógnita;
- o grau é 2, visto que o maior expoente da incógnita é 2.
Quando a equação do 2º grau está escrita na forma ax2 + bx + c = 0,dizemos que é a Forma Geral.
Exemplo:
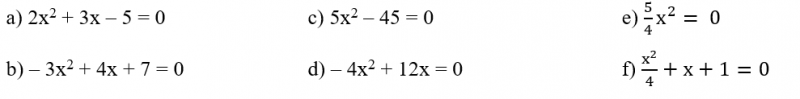
Nos exemplos acima:

OBS: Quando todos os coeficientes da equação do 2º grau são diferentes de zero, a equação é dita completa, logo será do tipo: ax2 + bx + c = 0.
Caso b e/ou c sejam iguais a zero, então: ax2 + c = 0, ax2 + bx = 0 ou ax2 = 0, as equações do segundo grau são do tipo incompletas.
CÁLCULO DO DISCRIMINANTE OU D (delta) DAS EQUAÇÕES DO 2º GRAU
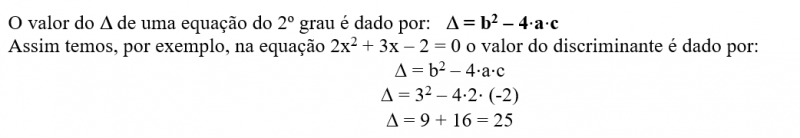
DISCUSSÃO DO NÚMEROS DE RAÍZES DE UMA EQUAÇÃO DO 2º GRAU

MÉTODO DE RESOLUÇÃO DAS EQUAÇÕES DO 2º GRAU
Para resolvermos uma equação do 2º grau laçaremos mão da fórmula de Bháskara.
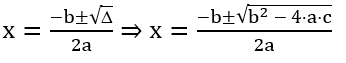

RESOLUÇÃO DE EQUAÇÕES DO 2º GRAU INCOMPLETAS
a) Com b = 0;
Se o valor de b é igual a zero, então a equação do 2º grau será do tipo ax2 + c = 0. Neste caso isola-se o valor de x, então teremos:
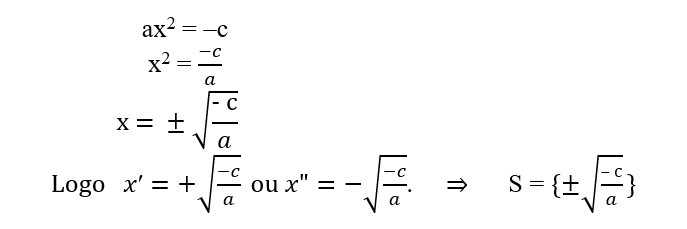

b) com c = 0;
Se o valor de c é igual a zero, então a equação do 2º grau será do tipo ax2 + bx = 0. Neste caso fatora-se a equação colocando o valor de x em evidência, então teremos:
ax2 + bx = 0
x (ax + b) = 0
Aplicando a Lei do Anulamento, se o produto de dois números reais m e p é igual a zero, então m = 0 ou p = 0, assim sendo temos:
Se x ( ax + b) = 0, então
x’ = 0 ou ax + b = 0
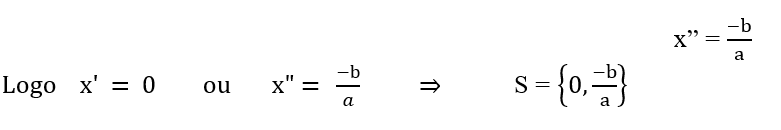
OBS: Se o valor se c for igual a zero então uma das raízes da equação do 2º grau será zero.
Exemplo: Resolva a equação incompleta 5x² – 3x = 0.
FORMA FATORADA DA EQUAÇÃO DO 2º GRAU
A forma toda equação polinomial do segundo grau do tipo ax2 + bx + c = 0, com raízes x’ e x”, pode ser fatorada da seguinte forma:
ax2 + bx + c = 0 a
(x – x’)
(x – x”) = 0
Exemplo: Escreva a equação geral do 2º grau de coeficiente dominante 1, sabendo que as raízes são:
a) x’ = 2 e x “ = 5
Na forma fatorada, temos:
a (x – x’)
(x – x”) = 0
1 (x – 2)
(x – 5) = 0
Aplicando a propriedade distributiva
x2 – 5x – 2x + 10 = 0
x2 – 7x + 10 = 0
Portanto a equação do 2º grau com coeficiente dominante 1 e de raízes 2 e 5 é x2 – 7x + 10 = 0
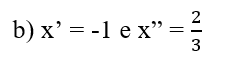

SOMA E PRODUTO DAS RAÍZES
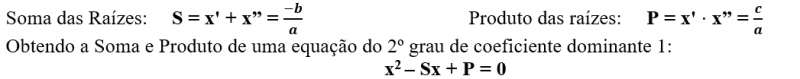
ATIVIDADES
01) Nas equações abaixo, determine o valor dos coeficientes a, b, c e o valor do discriminante:
a) 3x2 – 10x + 3 = 0
b) – x2 + 10x = 25
c) x2 = – 2x + 4
02) Determine os valores reais de m para que as equações abaixo na incógnita x sejam do 2º grau.
a) (m + 3)x2 – 10x + 3 = 0
b) (2m – 5)x2 + x + 4 = 0
c) (6 – 3m)x2 – 5x + 8 = 0
03) Determine o conjunto solução das equações do segundo grau na incógnita x.
a) x² – 7x + 10 = 0 d) 4x² – 20 = 0 g) 6x² + x – 1 = 0
b) x² – 8x + 12 = 0 e) -5x² + 4x = 0 h) 4x² + 9 = 12x
c) x² + 2x – 8 = 0 f) 2x² – 10x + 16 = 0 i) (x – 5)² = 1
04) Em sua aula, o professor de matemática propôs o seguinte problema: “A diferença entre o quadrado e o dobro de um mesmo número é 80”. Depois de um certo tempo seus alunos começaram a apresentar as soluções:
André disse que a solução era S = {-8, 10};
Bruna disse que a solução era S = {8, 10};
Carlos disse que a solução era S = {8, -10};
Débora disse que a solução era S = {-8, -10}
Ao resolver corretamente no quadro, o professor viu que:
A) ( ) André acertou.
B) ( ) Bruna acertou.
C) ( ) Carlos acertou.
D) ( ) Débora acertou.
05) O seguinte problema matemático foi encontrado em uma escavação arqueológica. “A diferença entre o dobro do quadrado de um número positivo e o triplo desse número é 77. Calcule o número.”
Querendo o arqueólogo resolver o problema deverá encontrar qual valor?

07) De a somente a soma e o produto das seguintes equações:
a) 2x2 – 6x – 11 = 0 c) 3x2 + 55 = 0 e) x2 – 6x + 12 = 0
b) 5x2 – 4x = 12 d) x2 – 6x = 0 f) x2 + 10x + 25 = 0
08) Sejam x1 e x2 as raízes da equação 10x2 + 33x – 7 = 0. O número inteiro mais próximo de 5x1x2 + 2(x1 + x2) é:
A) ( ) – 33
B) ( ) – 10
C) ( ) – 7
D) ( ) 10
09) Sabemos que a raiz de uma equação é um valor que atribuído a x satisfaz a igualdade. Em um caso particular, se a soma dos coeficientes (a + b + c) da equação do 2º grau for zero então 1 é uma de suas raízes (x’ = 1), e a outra raiz é dada por c/a (x” = c/a).
Nestas condições, verifique se “1” é raiz das equações abaixo. Em caso afirmativo, determine a outra raiz.
a) 3x2 – 10x + 7 = 0 c) 15x2 – 10x – 5 = 0 e) – x2 – x + 2 = 0
b) -4x2 + 9x – 5 = 0 d) – 4x2 – 10x + 14 = 0 f) 2021x2 – 1010x – 1011 = 0
10) Resolva as seguintes equações do 2º grau.