Estudo das grandezas e Regra de três – 9º Ano – 2ª Quinzena – 3º Corte – AULA e IMPRESSÃO - 16/09/2020
 Olá!! Vamos começar nossa atividade!!
Olá!! Vamos começar nossa atividade!!ESTUDO DAS GRANDEZAS
Uma Grandeza em matemática é tudo aquilo que pode ser medido e contado. Por exemplo, o tempo, a velocidade, o volume, a quantidade de homens em uma obra etc. O que não pode ser medido e nem contado não é uma grandeza. Exemplo: O amor, a saudade, a imaginação etc. Portanto, nosso estudo trata-se das grandezas mensuráveis (que podem ser medidas ou contadas) e da forma com a qual se relacionam.
Dizemos que duas grandezas “x” e “y” são diretamente proporcionais quando existe uma relação do tipo y = k∙x, com x positivo e “k” constante positiva, chamada de constante ou coeficiente de proporcionalidade.
Um exemplo que ilustra essa situação e a relação do espaço “S” e o tempo “T” em um movimento retilíneo e uniforme.
Exemplo: Um corpo em movimento retilíneo e uniforme tem velocidade constante e igual a 20 km/h. Isso significa dizer que, de acordo com a tabela a seguir, temos:
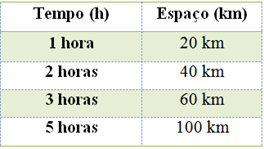
Note que à medida que o tempo aumenta o espaço aumenta na mesma proporção, ou seja, se o tempo dobra o espaço também dobra, se o tempo triplica o espaço também triplica etc.
A relação matemática entre o espaço e o tempo é dada por:
Na primeira expressão matemática, o quociente entre o espaço (S) e o tempo (T) é um valor constante igual a 20, o que nos revela uma importante relação entre Grandezas Diretamente Proporcionais (GDP):
Se duas grandezas são diretamente proporcionais então o quociente (divisão) entre elas é sempre um valor constante e positivo.
Na segunda expressão matemática, a relação entre o espaço (S) e o tempo (T) é do tipo y = k∙x, ou seja:
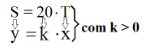
Dizemos que duas grandezas “x” e “y” são inversamente proporcionais quando existe uma relação do tipo y = k/x ou y∙x = k, com x > 0 e “k” constante positiva, ou seja, y é diretamente proporcional ao inverso de x.
Um exemplo que nos mostra esta situação e a relação da velocidade “V” e o tempo “T” em um movimento retilíneo e uniforme.
Exemplo: Um corpo em movimento retilíneo e uniforme percorre um espaço de 30 km. Isso significa que, de acordo com a tabela a seguir, temos:
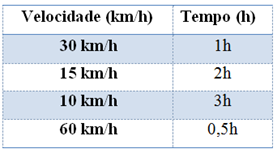
Neste caso, à medida que o tempo aumenta, a velocidade diminui na mesma proporção, ou seja, se o tempo dobra, a velocidade diminui pela metade, se o tempo triplica, a velocidade diminui para um terço, ou ainda, se a velocidade dobra o tempo diminui pela metade etc. A relação matemática entre a velocidade e o tempo é dada por:

Na segunda expressão matemática, o produto entre a velocidade (V) e o tempo (T) é constante “ k = 30”, um valor constante e positivo. Isso nos revela uma importante relação entre Grandezas Inversamente Proporcionais (GIP):
Se duas grandezas são inversamente proporcionais então o produto (a multiplicação) entre elas é sempre um valor constante e positivo.
Observação: Em uma relação do tipo:
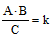
,sendo k > 0, entre as grandezas A, B e C temos que:
- A e B são inversamente proporcionais, o produto entre elas é constante, com C constante;
- A e C são diretamente proporcionais, o quociente entre ela é constante, com B constante.
Neste caso, a grandeza A é diretamente proporcional à C e inversamente proporcional B.
ESTUDO DAS ESCALAS
A escala numérica é utilizada pra representações de grandes medidas em um pequeno espaço. É baseada no quociente entre a medida no mapa e a medida real. Exemplo: Um mapa é dado na escala de 1: 200.000, significa dizer que cada centímetro no mapa é equivalente a 200.000 centímetros na distância real. Quando a escala não apresentar as unidades relacionadas, admite-se o centímetro como padrão.

É importante notar a relação de fração entre as duas grandezas lineares, ou seja, entre as distâncias. Quando a relação é entre áreas, medidas de superfície, a relação então fica:
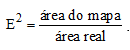
Atividades
01) Leia os itens a seguir e marque (V) para verdadeiro e (F) para falso.
a) ( ) Duas grandezas são diretamente proporcionais quando uma delas aumenta a outra, também, aumenta na mesma proporção.
b) ( ) Duas grandezas são diretamente proporcionais, quando uma delas diminui a outra aumenta na mesma proporção.
c) ( ) Duas grandezas são inversamente proporcionais, quando uma delas aumenta a outra diminui na mesma proporção.
d) ( ) Duas grandezas são inversamente proporcionais, quando uma delas diminui a outra, também, diminui na mesma proporção.
02) Leia os itens a seguir, marque a alternativa correta e reescreva as frases falsas, de modo que fiquem verdadeiras.
a) ( ) Se duas grandezas X e Y são tais que ao duplicarmos o valor de X, o valor de Y também duplica, então X e Y são grandezas inversamente proporcionais.
b) ( ) Se duas grandezas X e Y são tais que ao reduzirmos para um terço o valor de X, o valor de Y também reduz para um terço, então X e Y são grandezas inversamente proporcionais
c) ( ) Se duas grandezas X e Y são tais que ao triplicarmos o valor de X, o valor de Y fica reduzido para um terço do que era, então X e Y são grandezas inversamente proporcionais.
d) ( ) Se X é uma grandeza inversamente proporcional à grandeza Y, então Y é diretamente proporcional a X.
03) Aplicando o conhecimento de grandezas direta ou inversamente proporcionais, marque V para verdadeiro e F para falso. A seguir reescreva as frases falsas de modo que fiquem verdadeiras.

04) A tabela a seguir mostra a distância, em km e o tempo, em horas que um veículo levou para percorrer um trecho em uma rodovia. Verifique:
a) se as grandezas são diretamente proporcionais.
b) caso a resposta acima seja afirmativa, encontre a constante de proporcionalidade.

05) Determine, em cada caso, se a relação entre as grandezas é de proporção direta (D) ou inversa (I).
- O número de homens trabalhando e a quantidade de peças que eles produzem durante um mês. ( )
- O número de máquinas trabalhando e o tempo que levam para construir 1000 peças. ( )
- A velocidade de uma moto e o tempo que ele leva para fazer uma viagem de Brasília a Goiânia. ( )
- A velocidade de um caro e a distância percorrida por ele em cinco horas. ( )
- A quantidade de comida e o número de pessoas que podem ser alimentados com ela durante 1 ano( )
- O volume de uma garrafa de água e o tempo necessário para enchê-lo.( )
- O número de linhas por página e o total de páginas de um livro. ( )
- A habilidade de um grupo de trabalhadores e o tempo necessário para executarem certo serviço. ( )
- A dificuldade de uma obra e o tempo necessário para uma equipe executá-la. ( )
- A facilidade de uma tarefa e o tempo necessário para uma pessoa executá-la. ( )
- A quantidade de horas trabalhadas por dia e a quantidade de trabalho feito em uma semana. ( )
06) A proporção entre as medalhas de ouro, prata e bronze de um determinado país foi é 3:5:7, respectivamente. Quantas medalhas de ouro, prata e bronze espera-se que esse país obtenha em 90 jogos, se essa proporção se mantiver e ele conquistar medalhas em todos os jogos?
07) Numa fábrica, 16 homens com igual capacidade de trabalho, realizam uma tarefa durante 45 dias. Com 10 homens apenas, em quantos dias será realizada a mesma tarefa?
08) O texto abaixo traz algumas informações sobre a capital do nosso estado.
“Goiânia, a capital de Goiás, é a cidade mais populosa do estado, sua extensão territorial é de aproximadamente 733 quilômetros quadrados, e possui 1.302.001 habitantes.”
Fonte: www.ibge.org.gov
Sabendo que em uma escala temos a seguinte relação
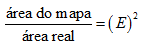
,ou seja, o quociente entre a área do mapa e a área real é igual ao quadrado do valor da escala. Se colocarmos a cidade de Goiânia em um mapa, na escala de 1:400 000, sua área corresponderia a
- ( ) 0,45812 cm2 .
- ( ) 4,5812 cm2.
- ( ) 45,812 cm2.
- ( ) 183,25 cm2.
09) A área do estado de Goiás pode ser obtida pelo seguinte processo: Coloca-se sobre uma folha de cartolina o mapa do estado e traça-se o seu contorno. Na mesma cartolina, desenha-se um quadrado de 10 cm de lado, conforme mostram as figuras.
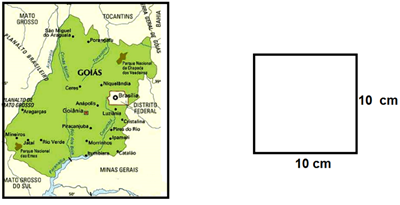
Disponível em: https://www.procuradoria.go.gov.br/noticias/
Consulta feita em 31/08/2020
Após serem recortadas, as duas figuras são pesadas em uma balança, que indica uma massa de 1 g para o quadrado de cartoluna e 8,502586 g para o mapa de Goiás, cuja escala é 1 : 2 000 000.
Desse modo, pode-se determinar a área desse Estado.
Nessas condições, a área do Estado de Goiás, em quilômetros quadrados, é, aproximadamente
- ( ) 65 143, 879
- ( ) 125.870,361
- ( ) 259.634,319
- ( ) 340.103,467
10) Em um mapa divulgado pela (ONG) Greepeace, uma área de desmatamento tem 20,3 hectares ( 20,3 hm2) na região sul do Amazonas.
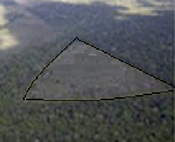

Fonte: www. greepeace.org/brasil
Querendo representar a área de degradação em um mapa, o professor Aislam considerou apenas 20 hectares e a região como um polígono triangular de 5 cm2.
Nestas condições, a escala utilizada pelo professor foi de
- ( ) 1 : 200.
- ( ) 1 : 2 000.
- ( ) 1 : 20 000.
- ( ) 1 : 4 000.
 Ufa!!! Concluímos…vamos revisar!!!
Ufa!!! Concluímos…vamos revisar!!! Baixe e imprima sua atividade!
Baixe e imprima sua atividade!