Estudo dos métodos de contagem (princípio fundamental da contagem) e aplicações no espaço amostral de eventos probabilísticos – Atividade 4 - 05/03/2021

Estudo dos métodos de contagem (princípio fundamental da contagem) e aplicações no espaço amostral de eventos probabilísticos.
A parte da matemática que estuda o número de possibilidades de um evento ocorrer é denominada de Análise Combinatória. Em uma linguagem simplificada, a Análise Combinatória é a arte de contar. Nem sempre contar é um processo simples. Por exemplo:
No sorteio da Mega-Sena são sorteadas 6 dezenas escolhidas entre os números inteiros 1 e 60. De quantas formas distintas pode-se fazer essa escolha?
Logo de início podemos perceber que existe um número muito grande de possibilidades para montarmos um jogo em uma cartela e que é necessária certa técnica para determinarmos quantas possibilidades existem.
No entanto, tendo feito um determinado número x de jogos, um apostador passa a ter a chance de acertar os números que serão sorteados. Perceba que quanto maior for a quantidade de x, maior será a chance de acertar e receber o prêmio. O cálculo de quanto é essa “chance” é denominado de probabilidade.
Entendemos portanto que, para calcular a quantidade de possibilidades de ocorrência de um determinado acontecimento usamos os métodos de contagem da Análise Combinatória. Porém, quando queremos saber qual a chance de acontecer um resultado ou um conjunto de resultados específicos em meio a todas as possibilidades existentes, estaremos diante a Probabilidade de ocorrência desse ou desses resultados.
Princípio Fundamental da Contagem
Princípio Fundamental da Contagem
Se um acontecimento ocorrer em “n” etapas distintas e independentes entre si, A = {E1, E2, E3, E4, … , En}, então o número total de possibilidades deste acontecimento ocorrer P(A) obtido fazendo-se o produto entre o número de possibilidades de ocorrência de cada etapa, ou seja, é:
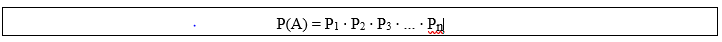
Onde:
⇔P1 é o número de possibilidades da 1ª etapa (E1);
⇔P2 é o número de possibilidades da 2ª etapa (E2);
⇔P3 é o número de possibilidades da 3ª etapa (E3);
⇔Pn é o número de possibilidades da n-ésima etapa (En);
Exemplo1). Para ir ao clube, Júnior deseja usar uma camiseta, uma bermuda e um par de tênis. Sabendo que ele dispõe de cinco camisetas, quatro bermudas e três pares de tênis, de quantas maneiras distintas poderá vestir-se?
Número de possibilidades para se vestir P(V) depende do número de possibilidades de cada etapa:
1ª Etapa: Escolha da camiseta = 5;
2ª Etapa Escolha da bermuda = 4;
3ª Etapa Escolha do tênis = 3,
P(A) = P1 ∙ P2 ∙ P3 = 5 ∙ 4 ∙ 3 = 60 possibilidades.
Nestas condições, Júnior possui 60 maneiras distintas para se vestir.
Exemplo 2). As atuais placas de licenciamento de automóveis constam de sete símbolos sendo três letras, dentre as 26 do alfabeto, seguidas de quatro algarismos. Quantas placas distintas podem ter sem o algarismo zero na primeira posição reservada aos algarismos?
Neste caso perceba que cada caractere da placa possui uma quantidade de escolhas possíveis.

Para a 1ª letra: 26 possibilidades de escolha;
Para a 2ª letra: 26 possibilidades de escolha;
Para a 3ª letra: 26 possibilidades de escolha;
Para o 1º algarismos: 9 possibilidades de escolha. (Note que não pode ser zero por condição do exercício);
Para o 2º algarismos: 10 possibilidades de escolha;
Para o 3º algarismos: 10 possibilidades de escolha;
Para o 4º algarismos: 10 possibilidades de escolha.
Portanto, pelo Princípio Fundamental da Contagem:
No de Placas = 26 x 26 x 26 x 9 x 10 x 10 x 10 = 158.184.000 placas possíveis.
Nestas condições, o número de placas possíveis é 158.184.000.
Probabilidade de um evento
Primeiramente temos que entender alguns conceitos preliminares.
⇒ Espaço amostral ( U ): é o conjunto de todos os resultados possíveis do experimento.
Por exemplo: O lançamento de um dado com seis faces.
Neste caso, o conjunto de possibilidades de resultados é U = {1, 2, 3, 4, 5, 6}.
Perceba que para um conjunto com muitas possibilidades de resultados podemos lançar mão da Análise Combinatória para contar o número de elementos desse conjunto.
⇒ Evento (E) é qualquer subconjunto do espaço amostral.
Por exemplo:
a) Evento 1 => faces números pares: {2, 4, 6};
b) Evento 2 => faces números múltiplos: {3, 6};
c) Evento 3 => faces números divisores de 60: {1, 2, 3, 4, 5, 6}.
d) Evento 4 => faces números múltiplos de 7: { }
Cálculo da Probabilidade:
Seja um espaço amostral U e E um de seus eventos, denomina-se probabilidade do evento E o número P(E) obtido fazendo-se o quociente entre o número de elementos do evento E e o número de elementos do espaço amostra (U).
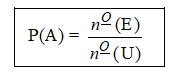
No exemplo acima:

Podemos perceber que se o evento tem todos os elementos do espaço amostral sua probabilidade é 1 ou 100% e é chamado de evento certo. Se o evento é uma subconjunto vazio do espaço amostral sua probabilidade é zero “0” e é chamado de evento impossível, assim:
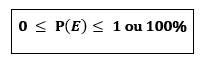
ATIVIDADES
01) Um grande prêmio de fórmula 1 vai ser disputado por 24 pilotos. De quantas formas distintas podemos montar o pódio com três pilotos.
02) Em um baralho de 52 cartas, uma carta é retirada aleatoriamente. Determine a probabilidade de a carta retirada ser:
a) um rei;
b) uma figura;
c) o rei de copas;
d) uma carta vermelha;
e) uma carta de copas;
f) o curinga.
03) Para uma missão no espaço, deverão ser escolhidos três super-heróis para a tarefa, sendo que:
•Um é homem e pode de voar;
•Um deve ser mulher;
•Um deve ter conhecimentos científicos.

Sabe-se que:
Superman, Lanterna-Verde e Caçador de Marte podem voar e que Batman e Flash são cientistas.
Nestas condições, de quantas formas distintas pode ser formada a equipe?
04) Durante a pandemia que começou em 2020, muitas empresas de vendas on-line, desenvolveram formas de atender seus consumidores buscando baratear o custo com o frete. Assim foram adotadas várias logísticas de transporte de mercadorias.
Observe o esquema, a seguir, que representa o número de caminhos disponíveis e os sentidos indicados das cidades A, B, C e D.
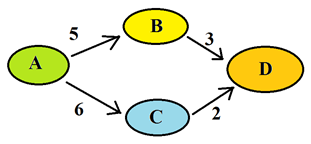
Suponha que um determinado produto seja produzido na cidade A e deve ser entregue na cidade D e que as cidades A, B, C e D possuem vários tipos de rotas para baratear o transporte dessas mercadorias até o consumidor.
Por exemplo: existem cinco rotas que vão de A para B; não existe rota direta de A para D.
Nessas condições, o número total de rotas distintas, de A até D é igual a
a) ( ) 16.
b) ( ) 36.
c) ( ) 27.
d) ( ) 28.
05) Numa mesa há 6 canetas que escrevem em azul, 7 em preto, 3 em vermelho e 4 que não possuem carga de tinta.
Escolhendo, ao acaso, uma dessas canetas, a probabilidade de que a caneta escolhida
a) escreva é __________________________________________________________
b) não escreva é _____________________________________________________
c) não escreva em azul é _____________________________________________
06) Uma senha é composta de 3 dígitos a serem escolhidos a partir do conjunto {A, B, C, D, E, F, G}. Quantas senhas distintas podem ser formadas de modo que:
a) as letras sejam escolhidas livremente;
b) as letras sejam escolhidas sem repetição.
07) Em um determinado jogo de tabuleiro, o jogador deve usar o símbolo do herói com o qual vai jogar, sendo que existem 20 possibilidades de personagens. O personagem é atribuído por meio de sorteio aleatório. João é muito fã do “Batman” e do Capitão América.
Nestas condições, a probabilidade de João jogar com seus personagens preferidos está entre:
a) ( ) 5% e 15%.
b) ( ) 15% e 25%.
c) ( ) 25% e 35%.
d) ( ) 35% e 40%.
08) Considerando os números de 1 até 100, qual a probabilidade de escolhermos um número múltiplo de 8?
09) Uma máquina contém pequenas bolas de borracha de 20 cores diferentes, sendo 5 bolas de cada cor. Ao inserir uma moeda na máquina, uma bola é expelida ao acaso. Nestas condições, qual é a probabilidade de se retirar uma bolinha da cor azul?
a) ( ) 20%
b) ( ) 15%.
c) ( ) 10%.
d) ( ) 5%.
10) Num carro com 5 lugares e mais o lugar do motorista viajam 6 pessoas, das quais 2 sabem dirigir. Nestas condições, quantas maneiras se pedem dispor essas 6 pessoas em viagem?
Não esqueça de imprimir sua atividade!
