Gráficos de barras, colunas, linhas ou setores e seus elementos constitutivos e adequação para determinado conjunto de dados: Medidas de centralidade – Atividade 9 - 19/05/2021
GRÁFICOS
Com muita frequência encontramos algumas reportagens em jornais ou revistas em que as informações são colocadas utilizando figuras ilustrativas, os gráficos. A finalidade desses gráficos é facilitar a compreensão das informações ou reforçar matematicamente os dados apresentados. Essas imagens facilitam o entendimento da informação a partir de uma análise visual das figuras apresentadas, possibilitando a explicação de muitas informações apenas por uma apresentação visual, fazendo com que o leitou entenda rapidamente a informação apresentada.
Temos alguns gráficos clássicos: colunas, barras, setores, linha e pictogramas.
Gráfico de Barras
São usados retângulos paralelos, horizontais ou verticais. As larguras das barras são sempre iguais, porém o comprimento é diretamente proporcional à frequência dos elementos apresentados.
Exemplo: Devido a pandemia causada pelo vírus Covid – 19, algumas cidades do país apresentaram os seguintes índices de isolamento social.

Esses valores podem ser representados no gráfico a seguir.
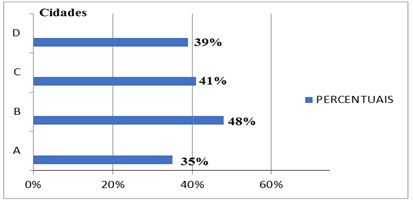
Note que o comprimento das barras é diretamente proporcional às porcentagens apresentadas. Neste caso é possível perceber que a finalidade do gráfico é fazer uma comparação entre as frequências dos elementos.
Gráfico de Colunas
São usados retângulos paralelos e verticais. As larguras das colunas são sempre iguais, porém, assim como o de barras, o comprimento é diretamente proporcional à frequência dos elementos apresentados. As colunas devem ser igualmente espaçadas. Ainda temos que o gráfico faz uma comparação prática entre as frequências dos elementos.
Exemplo: Em uma pesquisa feita com 20 alunos a respeito do gênero literário com maior preferência, foram coletados os seguintes dados:
- 8 alunos preferem ação;
- 3 alunos preferem comédia;
- 4 alunos preferem drama;
- 5 alunos preferem suspense.
Esses dados podem ser organizados no gráfico a seguir.
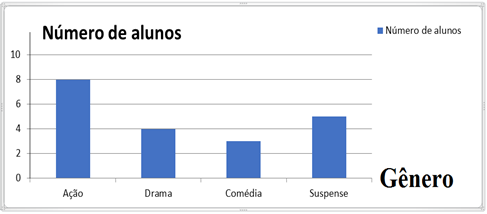
Gráfico de Setores ou de Pizza
Nesta modalidade de gráfico cada elemento é colocado como uma componente em um setor circular, assim a finalidade deste tipo de gráfico é mostrar uma comparação das quantidades de cada elemento entre si e em relação ao total de elementos na pesquisa. Portanto a medida do ângulo central de cada setor é diretamente proporcional à frequência relativa do elemento, ou seja, o valor do ângulo central do setor é proporcional à porcentagem.
Exemplo: Considere a safra nacional de certo cereal, no ano passado. Sua produção foi disposta na tabela a seguir apontando a participação por região do país.
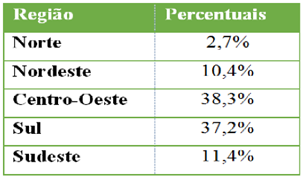
Ilustre a participação de cada região na produção deste cereal por meio de um gráfico de setores.
Solução: Esses dados podem ser representados no gráfico de setores a seguir.
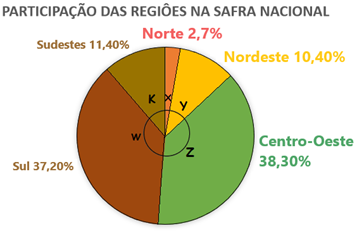
Note que o ângulo central é diretamente proporcional à porcentagem da participação de cada região.

Gráfico de Linhas
Este tipo de gráfico é usado para indicar o desempenho de determinados elementos ao longo de um período.
Exemplo: As intenções de votos de determinados candidatos à presidência do conselho regional de medicina podem ser representadas no gráfico a seguir.
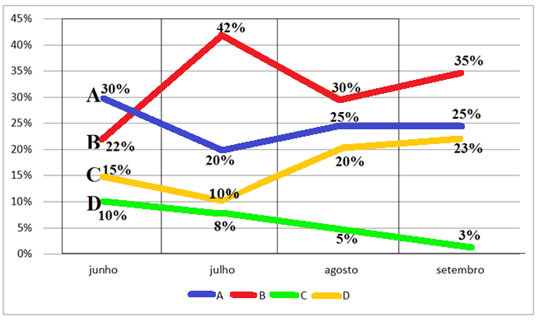
Neste gráfico é possível notar a evolução das intenções de votos de cada candidato ao longo de quatro meses.
Medidas de Centralidade ou Medidas de Tendência Central
São usadas para indicar uma tendência nos resultados ou no comportamento de uma pesquisa. Dentre elas temos a Média Aritmética e a Moda.
Média Aritmética Simples por definição é a soma dos valores de todos os termos de uma pesquisa, divida pelo número de termos.
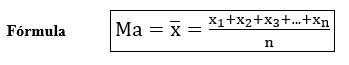
Em que:
Ma = : média aritmética simples;
x1, x2, x3,…, xn: valores dos termos ou dos dados;
n: número de termos ou de dados.
Média Aritmética Ponderada por definição é a soma dos valores de todos os termos de uma pesquisa dividida pelo número de termos, porém neste caso, é possível multiplicar o valor do elemento pelo número de vezes que ele aparece na pesquisa, ou seja, é possível multiplicar cada elemento por sua frequência absoluta.
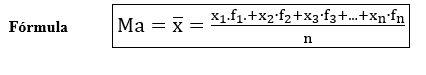
Em que:
Ma = : média aritmética simples;
x1, x2, x3,…, xn: valores dos termos ou dos dados;
f1, f2, f3,…, fn: é o número de vezes que os valores apareceram na pesquisa;
n: número de termos ou de dados, ou seja, n = f1 + f2 + f3 +…+ fn.
Moda (Mo)
É uma medida de centralidade que indica o termo com maior frequência em uma pesquisa.
ATIVIDADES
01) As 10 medidas colhidas por um cientista num determinado experimento, todas na mesma unidade, foram as seguintes: 1,2; 1,2; 1,4; 1,5; 1,5; 2,0; 2,0; 2,0; 2,0; 2,2.
Ao trabalhar na análise estatística dos dados, o cientista determinou a média e a moda dos dados.
Dessa forma, os resultados obtidos pelo cientista em sua análise estatística
A) ( ) a moda é 1,2 e a média é 1,6.
B) ( ) a moda é 1,2 e a média é 1,7.
C) ( ) a moda é 2,0 e a média é 1,7.
D) ( ) a moda é 2,0 e a média é 1,6.
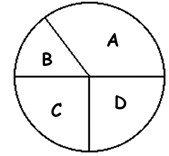
02) Os resultados de uma pesquisa de opinião foram divulgados utilizando um gráfico de setores circulares, como o representado na figura a seguir.
Os setores assinalados com A, B, C e D, representam de forma percentual as quatro possíveis escolhas da pesquisa.
De acordo com essa pesquisa a moda está associada ao setor
A) ( ) A.
B) ( ) B.
C) ( ) C.
D) ( ) D.
03) No ano passado em um determinado Estado obteve uma redução no número de acidente sem vítimas fatais e os dados foram anotados na tabela a seguir:
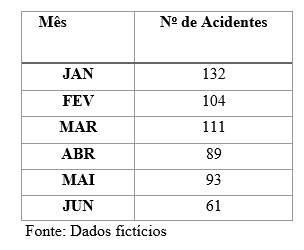
Utilizando os dados da tabela acima construa um gráfico para ilustrar o desenvolvimento do número de acidentes ao longo do primeiro semestre do ano passado.
04) Em uma sala com 72 alunos, um professor aplicou um teste em que as notas eram qualificadas por letras e o resultado foi colocado na tabela a seguir.
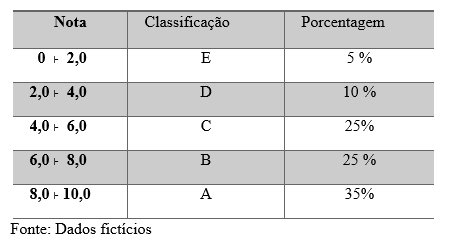
Utilizando os dados da tabela acima construa um gráfico para ilustrar a participação de cada nota em relação a toda a turma.
05) Em um campeonato de basquete o artilheiro do colégio, Gabriel, marcou em uma sequência de oito jogos consecutivos, a seguinte pontuação: 43, 35, 38, 35, 39, 29, 35 e 30.
De acordo com esses dados, determine:
a) A média aritmética dos pontos de Gabriel nos 8 jogos;
b) A moda dos pontos nessas partidas.
06) De acordo com atividade anterior, responda:
Se na próxima partida Gabriel marcar 50 pontos, o que ocorrera com sua média de pontos? Ela aumenta, diminui ou não irá se alterar?
07) Uma pesquisa com 21 pacientes que estava internados em um hospital, realizada pela direção da instituição, avalia a redução dos custos hospitalares mensais individuais em função do bem-estar emocional promovido pela vivência de atividades de entretenimento.
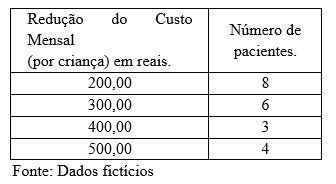
Com base nos dados descritos na tabela, determine a redução média dos custos.
08) Utilizando os dados da tabela anterior, construa um gráfico para melhor representar o número de pacientes em relação à redução de custos hospitalares.
09) A média aritmética ponderada de idade de uma turma de uma escola em que há 10 pessoas de 15 anos, 8 pessoas de 17 anos e 6 de 18 anos de idade está entre
A) ( ) 15,0 e 15,5 anos.
B) ( ) 15,5 e 16,0 anos.
C) ( ) 16,0 e 16,5 anos.
D) ( ) 16,5 e 17,0 anos.
10) As notas de 5 alunos em uma prova de matemática foram as seguintes: 6, 8, 8, 3 e 7. Nestas condições, o valor da média alcançada por esses alunos e a moda das notas foi
A) ( ) Ma = 6,3 e Mo = 6.
B) ( ) Ma = 6,4 e Mo = 8.
C) ( ) Ma = 6,5 e Mo = 7.
D) ( ) Ma = 6,6 e Mo = 8.
“Cada lição que você deixa de estudar é uma parte
do seu futuro grandioso que deixa de existir”
Steve Jobs
