Matemática – 9º Ano – Conjunto dos Números Reais (ℝ) – 1ª quinzena – 3º corte – IMPRESSÃO - 02/09/2020
 Olá!!! vamos iniciar a atividade!!!
Olá!!! vamos iniciar a atividade!!!Conjunto Dos Números Reais
O conjunto dos números reais é representado pelo símbolo ℝ e é formado pela união do conjunto dos números racionais com o conjunto dos números irracionais. Lembre-se de que o conjunto dos racionais é a união dos conjuntos naturais e inteiros. Ao dispormos os números reais em uma reta, temos que o número zero é a origem da reta, à direita do zero estarão os números positivos, e à esquerda, os números negativos.
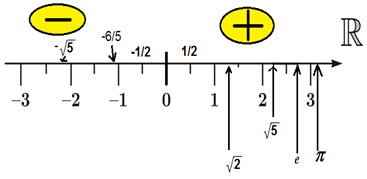
Como esse eixo é real, podemos dizer que entre dois números existem infinitos números e que esse eixo é infinito tanto na direção positiva quando na direção negativa.
Notação Científica: Uma maneira de uniformizar a forma de escrever valores, que pode ser usada com igual eficiência tanto para números muito grandes, quanto para números muito pequenos é chamada de notação científica. É importante lembra que estamos utilizando as propriedades de potenciação para trabalharmos com as notações científicas.
Essa forma de representação utiliza números naturais de 1a 9, com 1 ≤ x ≤ 9, multiplicado por potências de base 10 com expoentes inteiros (ora positivos, ora negativos).
Exemplos:
a) A velocidade da luz é em torno de 300.000 de km/s ou 300.000.000 m/s. Esse valor pode ser escrito como sendo 300. 000. 000 m/s = 3×108 m/s
Note que a vírgula se deslocou 6 casas para a esquerda, logo, em notação científica temos 3×108 m/s.
b) A medida de um raio atômico, é em geral, medido em nanômetros (1 nanômetro é igual à bilionésima parte de um metro (10-9 m)).
Portando um nanômetro é 0,000 000 001m, em notação científica teremos 1,0 x 10-9 m.
Note que a vírgula se deslocou 9 casas para a direita, logo, em notação científica é 1,0 x 10–9.
Propriedades da Potenciação
P1) Multiplicação de potências de mesma base: conserva-se a base e somam-se os expoentes.
Exemplo: 52x53 = 52+3 = 55, isso fica evidente vendo que 52 = 5×5 e 53 = 5x5x5, logo: 52x53 = 5x5x5x5x5 = 55.
P2) Divisão de potências de mesma base: conserva-se a base e subtraem-se os expoentes. Exemplo:
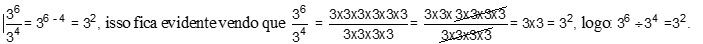
P3) Potência de potência: conserva-se a base e multiplicam-se os expoentes. Exemplo:
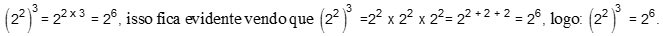
P4) Multiplicação de base diferentes elevadas ao mesmo expoente: multiplicam-se as bases elevadas ao respectivo expoente. Exemplo:
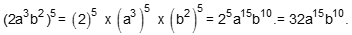
P5) Divisão de base diferentes elevadas ao mesmo expoente: dividem-se as bases elevadas ao respectivo expoente. Exemplo:
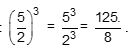
P6) Quando uma potência muda de posição em uma fração: vai de numerador para denominador ou de denominador para numerador: muda-se o sinal do expoente. Exemplo:

ATIVIDADES
01) Sabemos que os números podem ser ordenador em um eixo numérico que é denominado eixo real. Neste caso considera-se que cada número corresponde a um único ponto no eixo real e a recíproca é verdadeira, ou seja, cada ponto do eixo também corresponde a um único número real. Tomemos os valores para x = 7/5, y = √2 e z = 1,5. Nestas condições temos que
a) ( ) z < x < y.
b) ( ) y < x < z.
c) ( ) x < z < y.
d) ( ) x < y < z.
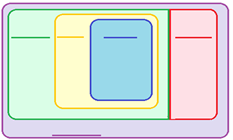
02) O conjunto dos números complexos é o conjunto que envolve todos os outros conjuntos numéricos. O diagrama abaixo pode ser usado para representar a relação do contém/contido, existentes entre os conjuntos numéricos. Deste modo preencha corretamente o diagrama abaixo, colocando pelo menos dois exemplos em cada conjunto.
03) A quantidade de números inteiros positivos, localizados entre 10 e 2020, que são múltiplos de 11 é
a) ( ) 184.
b) ( ) 183.
c) ( ) 182.
d) ( ) 181.
04) Escreva os números abaixo usando a forma de notação científica:
a) 320 000 000 000 000 000 000 =
b) 0, 000 000 038 =
c) 125 000 000 000 =
d) 0,001 =
e) 0, 000 000 000 000 000 000 000 023 =
f) 80.000 =
05) Escreva os números abaixo em notação científica, usando as potências de base 10.
a) 100 = b) 10.000 =
c) 0,1 = d) 0,01 =
e) 1.000.000 = f) 0,000 1 =
06) A notação científica é muito usada para uniformizar as representações.
Se x = 0,000013 = 1,3 ∙ 0,00001, escreva o número x usando potência de 10 com expoente inteiro negativo.
07) Aplicando a propriedade das potências, simplifique a expressão:
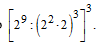
08) Aplicando as propriedades das potências de mesma base, simplifique as expressões:
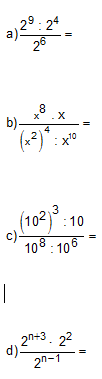
09) Simplifique a expressão
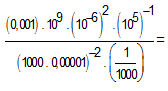
 Leia o texto a seguir.
Leia o texto a seguir.Nanotecnologia e a Impermeabilização
“A nanotecnologia está se tornando cada vez mais presente nas coisas do dia a dia. Recentemente foi lançado para comercialização um spray impermeabilizante que aplica uma camada de vidro líquido hidrofóbico 500 vezes mais fina que um fio de cabelo sobre a superfície a ser impermeabilizada, impedindo que a água e a sujeira entrem em contato direto com o objeto.
O spray impermeabilizante pode ser usado em vários locais, tais como: bancos de carro, sofás, roupas, objetos e superfícies que desejamos proteger da água.
Há estudos para o uso desta tecnologia para deixar equipamentos eletrônicos, como o celular, impermeabilizados, até mesmo a prova da água em grandes profundidades.”
Fonte: Canaltech, 5 invenções da nanotecnologia (adaptado), disponível em: http://bit.ly/2p0zdWWAcesso em: 24/08/2020
10) Com base nas informações do texto responda as questões:
a) Sabendo que um fio de cabelo tem em média diâmetro de 6 ∙10-5 metros. Calcule a espessura da camada do impermeabilizante.
b) Um livro de 300 páginas que tivesse cada uma de suas páginas impermeabilizadas dos dois lados da folha, teria um aumento de quantos milímetros em sua largura total? Esse aumento seria perceptível pelos leitores?
11) Leia esta manchete:
“Cientistas britânicos conseguiram fazer com que um microscópio ótico conseguisse enxergar objetos de cerca de 0,000 000 05 m, oferecendo um olhar inédito sobre o mundo ‘nanoscópico”.
Sobre o texto acima responda:
a) Um objeto que tem o comprimento de cerca de 0,000 000 05 m tem que medida em notação científica, usando o metro com unidade?
b) O microscópio referido no texto acima, é capaz de enxergar até quantos nanômetros?
12) Simplifique a expressão e escreva o resultado em notação científica
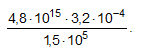
 Muito bom!!! Vamos revisar agora!!!
Muito bom!!! Vamos revisar agora!!!
 Baixe o arquivo e faça a impressão da atividade!!!
Baixe o arquivo e faça a impressão da atividade!!!