MEDIDAS DE GRANDEZAS

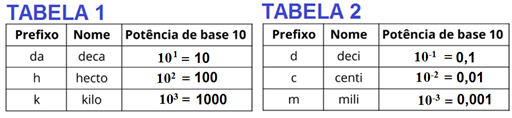
         Em 1960 com o surgimento do Sistema Internacional de Unidades, a unidade de medida de distância (comprimento) que ficou padronizada é o metro (m). Para expressarmos distâncias maiores que o metro usamos os múltiplos do metro que são o decâmetro, o hectômetro e o quilômetro. Para trabalharmos com medidas menores que o metro então usamos os submúltiplos do metro que são o decímetro, o centímetro e o milímetro. Veja a tabela abaixo.

         Na tabela temos os múltiplos e os submúltiplos do metro e seus valores em base 10. Os prefixos mais usados para os múltiplos do metro estão na tabela 1 e os mais usados para expressar os submúltiplos do metro estão na tabela 2. 

Uma regra prática para efetuarmos a conversão das unidades de medida é

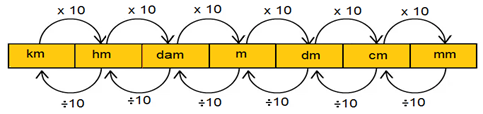
Note que, para irmos de medidas maiores para menores a cada unidade, multiplicamos o valor a ser convertido por 10.

Exemplo 1: Converta 2 km para  metros.

Temos:  2km = 20 hm = 200 dam = 2.000 m.

Neste caso,  multiplicamos por 10 três vezes porque se deslocam três casas para a direita.

Veja que para irmos de medidas menores para maiores a cada unidade, dividimos o valor a ser convertido por 10.

Exemplo 2: Converta 5 cm para metros.

Temos: 5 cm = 0,5 dm = 0,05 m.

Note que dividimos por 10 duas vezes porque se deslocam duas casas para a direita.

ASSISTA O VIDEO ANTES DE INICIAR AS ATIVIDADES…

https://vimeo.com/user19921347/review/426752798/657e408d0d

IMPORTANTE: para abrir o vídeo utilize a senha: vamosaprender

Atividades

1. Transforme as medidas a seguir.

a) 3 metros em centímetros.

b) 120 metros em quilômetros.

c) 5,4 quilômetros em metros.

02. Associe cada item da coluna da direita com os itens da coluna da esquerda, lembrando que só é possível somar valores que estão nas mesmas unidades. Quando as unidades forem diferentes é preciso igualá-las.

(a) (  ) 3,6 km + 450 m;                          (1) 6.766 dm

(b) (  ) 6,8 hm – 0,34 dam;                     (2) 4.050 m

(c) (  ) 16 dm + 54,6 cm + 200 mm       (3) 2.346 mm

Nestas condições, a associação correta será

a) (  ) a e 1; b e 2; c e 3.

b) (  ) a e 3; b e 2; c e 1.

c) (  ) a e 2; b e 1; c e 3.

d) (  ) a e 1; b e 3; c e 2.

03) Preciso colocar três voltas de arame farpado em volta de uma chácara retangular que mede 0,6 km de medida de fente (largura)  e 0,5 km de medida de fundo (comprimento).

Nestas condições, quantos metros de arame farpado devo compar?

a) (  ) 2200 m           

b) (  ) 3300 m          

c) (  ) 6000 m           

d) (  ) 6600 m

04) “Um byte, frequentemente confundido com bit, é um dos tipos de dados integrais em computação. É usado com frequência para especificar o tamanho ou quantidade da memória ou da capacidade de armazenamento de um computador, independentemente do tipo de dados armazenados. A codificação padronizada de byte foi definida como sendo de 8 bits.“

Disponível em: https://www.adassoft.com/unidade-de-medida-em-informatica-byte-quilobyte-megabyte-gigabyte/ Acesso em 15 de agost. De 2020.

De acordo com o texto, se um determinado arquivo tem o tamanho de 1600 bits, então é correto afirmar que ele terá o equivalente a

a) (  ) 20 bytes.

b) (  ) 200 bytes.

c) (  ) 2000 bytes.

d) (  ) 160 bytes.

05) A cada conjunto de 8 bits damos o nome de byte. Isso ocorre porque geralmente os computadores são idealizados para armazenar instruções em múltiplos de bits, que foram chamados de bytes.

Disponível em: https://www.somatematica.com.br/curiosidades/c119.php Acesso em 15 de agost. De 2020.

As unidades maiores são todas múltiplas do byte, como o kilobyte (ou quilobyte). É importante entender que embora o prefixo quilo signifique 1000, o termo quilobyte e o símbolo kB têm sido usados na área da computação para se referir a 1024 (2¹⁰) bytes que é pouco maior que 1000 (10³) bytes. Consequentemente  a partir daí, a contagem normalmente é feita em relação a 1024, ou seja, 1kB (kilobyte) corresponde a 1024 bytes e assim por diante:

1 kilobyte (kB) = 1024 bytes

1 megabyte (MB) = 1024 kilobytes

1 gigabyte (GB) = 1024 megabyte

1 terabyte(TB)= 1024 gigabyte.

Nestas condições, podemos dizer que 20 TB são equivalentes à

a) (  ) 1.024 GB.

b) (  ) 1.048  GB.

c) (  ) 20.240 GB.

d) (  ) 20.480 G

06) A tabela abaixo mostra as distâncias de alguns planetas ao Sol e uma escala para uma possível representação em uma folha ou na página de um livro. Note que algumas distâncias em escala foram representadas por “x” e “y”.

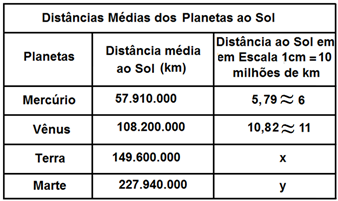
Nestas condições, os valores inteiros mais próximos de “x” e “y” são respectivamente

a) (  ) 14 e 22.

b) (  ) 15 e 23.

c) (  ) 14 e 23.

d) (  ) 15 e 22.

MEDIDAS DE TENDÊNCIA CENTRAL (MÉDIA, MEDIANA E MODA)

         Média Aritmética Simples por definição é a soma dos valores de todos os termos de uma pesquisa divida pelo número de termos.  

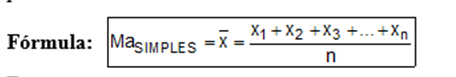
Em que:

M_a = : média aritmética simples;

x₁, x₂, x₃,…, x_n: valores dos termos;

n: número de dados.

Exemplo: Em uma rodada de um campeonato de futebol estadual foram realizadas cinco partidas, e os placares são: jogo 1→ 2×1; jogo 2 → 1×0, jogo 3 → 3×1; jogo 4 → 2×2 e jogo 5 → 1×1.

Nestas condições, qual foi a média de gols obtida nesta roda do campeonato?

Solução: jogo 1→ 3 gols; jogo 2 → 1 gol, jogo 3 → 4 gols; jogo 4 → 4 gols e jogo 5 → 2gols, portanto,

Portanto a média desta rodada do campeonato foi de 2,8 gols.

Em que:

M_p: Média aritmética ponderada.

x₁, x₂,…,x_n: valores dos elementos.

fa₁, fa₂,…, fa_n: são as frequências absolutas dos elementos ou o número de vezes que cada elemento aparece na pesquisa.

n: número de elementos na pesquisa que é a soma das frequências absolutas.

Exemplo: Um museu encomendou uma pesquisa para saber as dimensões de algumas peças que seriam expostas. Para essa pesquisa foram utilizadas 50 peças  decorativas com alturas diferentes. A tabela mostra o número de peças e suas respectivas alturas.

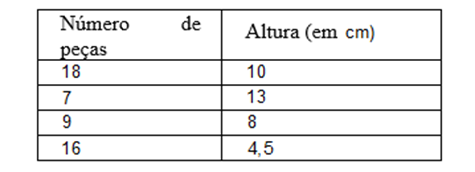
          Considerando os valores da tabela, determine  a média aritmética das alturas das peças desse conjunto.

Solução: Note que:  18 peças têm a altura de 10 cm; 7 peças têm a altura de 13 cm; 9 peças têm a altura de 8 cm; 9 peças têm a altura de 8 cm, e que, a altura de 4,5 cm aparece 16 vezes na pesquisa.

Assim, a média aritmética ponderada é dada por:

Note que a soma do número de vezes que cada medida apareceu na pesquisa (18 + 7 + 9 + 16) é o número de elementos da pesquisa.

Portando a média das alturas das peças será de 8,3 cm.

07) A distribuição de frequências das notas dos alunos de uma classe, em uma certa disciplina, é dada a seguir.

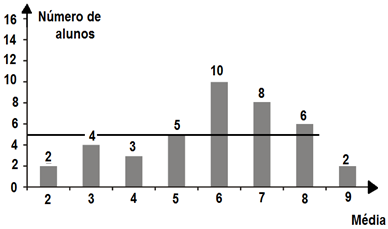
De acordo com esse texto, determine a média aritmética dessa turma.

a) (  ) 7,875

b) (  ) 6,875

c) (  ) 5,875 

d) (  ) 4,875 

Moda: É o valor ou a característica mais frequente de um conjunto, ou seja, é o dado que mais aparece na pesquisa. Na atividade 7, a moda das notas da turma é 6, porque é a nota que tem maior frequência.

Mediana: É o valor que divide um conjunto numérico ordenado ao meio, ou seja, em um conjunto organizado de ordem crescente ou decrescente o valor da mediana é aquele que divide o conjunto exatamente ao meio ou o valor central.

Exemplo: Em uma turma de  pós graduação com nove alunos suas idades foram: 32, 33, 26, 31, 44, 52, 32, 20 e 32 anos.

Para encontrar a mediana das idades dessa turma, devemos organizar a lista de idades em ordem crescente:

20, 26, 31, 32, 32, 32, 33, 44 e 55. Observe que o número 32 é o quinto. À sua direita, existem outras 4 idades, assim como à esquerda.

20, 26, 31, 32, 32, 32, 33, 44, 55

Logo, Me = 32 é a mediana das  idades dos alunos da turma.

Se a lista ordenada possuir um número “n” par de números, para encontrar a mediana (Me), devemos encontrar os dois valores centrais (x_n/2 e x_(n/2)+1) da lista, somá-los e dividir o resultado por 2.

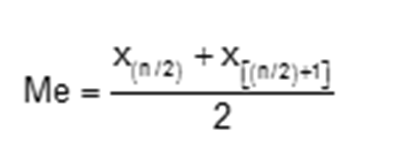
Exemplo: Na questão 07, as notas dos alunos, escritas de forma ordenada, foram:

2, 2, 3, 3, 3, 3, 4, 4, 4, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 7, 7, 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 8, 8, 9 e 9

Como são 40 números a mediana deve ser calculada fazendo a média aritmética entre os dois números centrais, que são x_40/2 e x_(40/2)+1 ou seja, x₂₀ e x_21. Assim,

08) A tabela abaixo mostra os valores de condomínios pagos pelos apartamentos de em um complexo residencial situados em uma determinada área na capital.

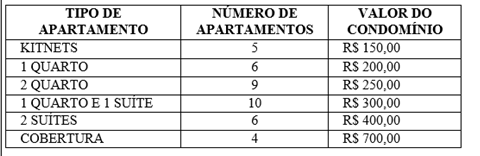
Com base nessa tabela, determine a média aritmética, a mediana e a moda desses valores cobrados pelo condomínio.

09) Após a aplicação de uma prova de Matemática, em uma turma de Ensino Médio com 30 estudantes, o professor organizou os resultados, conforme a tabela a seguir.

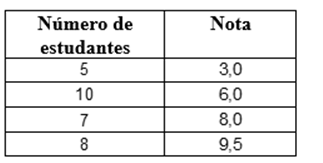
A nota média aritmética, a mediana e a moda dos resultados dessa prova de Matemática foram

a) (  ) Ma =  6,9  ,   Me = 7,0 e Mo = 6,0

b) (  ) Ma =  7,0  ,  Me = 6,9 e Mo = 6,0     

c) (  ) Ma =  6,9  ,  Me = 8,0 e Mo = 8,0     

d) (  ) Ma =  7,0  ,  Me = 8,0 e Mo = 9,5     

Você também pode imprimir essa aula!!