PROPRIEDADES DA POTENCIAÇÃO

P1) Multiplicação de potências de mesma base: conserva-se a base e somam-se os expoentes.

Exemplo: 5²x5³ = 5²⁺³ = 5⁵, isso fica evidente vendo que 5² = 5×5 e 5³ = 5x5x5.

Logo: 5²x5³ = 5x5x5x5x5 = 5⁵.

P2) Divisão de potências de mesma base: conserva-se a base e subtraem-se os expoentes.

Exemplo:

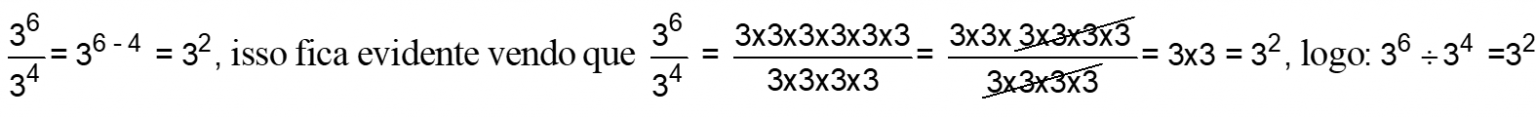
P3) Potência de potência: conserva-se a base e multiplicam-se os expoentes.

Exemplo:

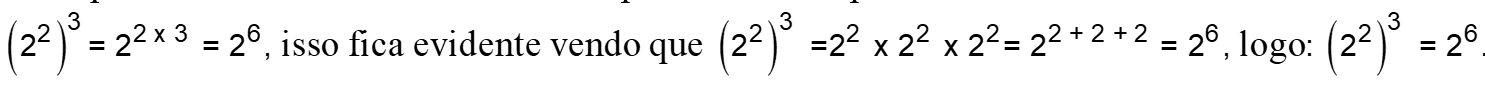
P4) Multiplicação de base diferentes elevadas ao mesmo expoente: multiplicam-se as bases elevadas ao respectivo expoente.

Exemplo:

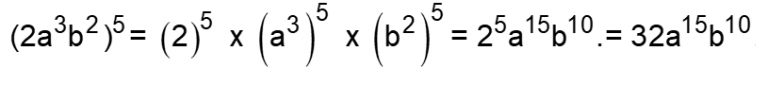
P5) Divisão de base diferentes elevadas ao mesmo expoente: dividem-se as bases elevadas ao respectivo expoente Exemplo:

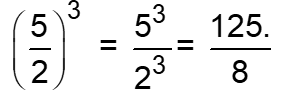
P6) Quando uma potência muda de posição em uma fração: vai de numerador para denominador ou de denominador para numerador: muda-se o sinal do expoente.

Exemplos:

VAMOS CONTINUAR! 

NOTAÇÃO CIENTÍFICA

Uma maneira de uniformizar a forma de escrever valores, que pode ser usada com igual eficiência tanto para números muito grandes, quanto para números muito pequenos é chamada de notação científica. É importante lembra que estamos utilizando as propriedades de potenciação para trabalharmos com as notações científicas.

Essa forma de representação utiliza números naturais de 1a 9, com 1 ≤ x ≤ 9, multiplicado por potências de base 10 com expoentes inteiros (ora positivos, ora negativos).

Exemplos:

a) A velocidade da luz é em torno de 300.000 de km/s ou 300.000.000 m/s. Esse valor pode ser escrito como sendo 300. 000 m/s = 3×10⁸ m/s

Note que a vírgula se deslocou 6 casas para a esquerda, logo, em notação científica temos 3×10⁸ m/s.

b) A medida de um raio atômico, é em geral, medido em nanômetros (1 nanômetro é igual à bilionésima parte de um metro(10^-9 m)).

Portando um nanômetro é 0,000 000 001m, em notação científica teremos 1,0 x 10^-9 m.

Note que a vírgula se deslocou 9 casas para a direita, logo, em notação científica é 1,0 x 10^–9.

RADICIAÇÃO

Definição: Dados um número natural n (com n 2), chama-se raiz n-ézima de a o número real b, tal que:

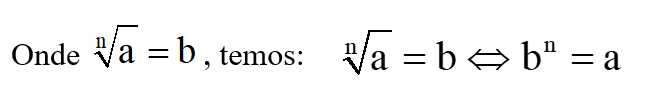
Propriedades:

1 – Multiplicação de radicais de mesmo índice: Conserva-se o índice e multiplicam-se os radicandos:

Exemplos:

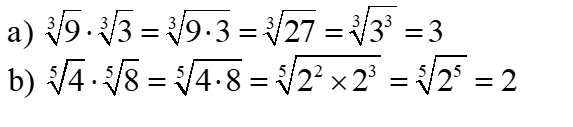
2 – Divisão de radicais de mesmo índice: Conserva-se o índice e dividem-se os radicandos;

Exemplos:

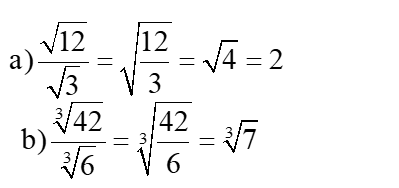
3 – Radical de um radical: Conserva-se o radicando e multiplicam-se os índices.

Exemplos:

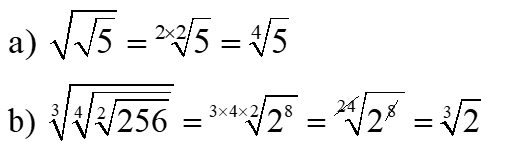
4 – Radicais equivalentes: Quando se multiplica ou se divide o índice do radical e o expoente do radicando por um mesmo número real diferente de zero, obtém-se um radical equivalente:

Exemplos:

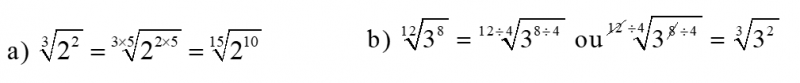
RACIONALIZAÇÃO DE DENOMINADORES

ATIVIDADES

1. Escreva as seguintes quantidades de grandezas a seguir, na forma de notação científica:

a) 560 000 000 000 000 000 000 m =

b) 0, 000 000 000 000 000 8 g = 

c) 745 000 000 000 L=

d) 31415949232471 s =

e) 0, 000 000 000 000 000 46 kg =

f) 80.400 mL =

2. Escreva os números a seguir, em notação científica, usando as potências de base 10.

a) 1000 =

b) 10.000.000 =

c) 0,001 =

d) 0,01 =

e) 1.000.000 =

f) 0,0001 =

3. Qual desses números é igual a 0,064?

a (   )  ( 1/80 )²

b) (   )  ( 1/8 )²

c) (   ) ( 2/5 )³

d) (   ) ( 1/800 )²

e) (    ) ( 8/10 )³  

4. Aplicando a propriedade das potências, simplifique a expressão

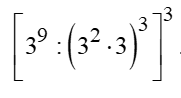
05) Simplificando a expressão a seguir, obteremos:

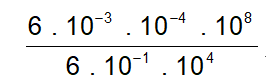
a) (   ) 10⁰

b) (   )10^-1

c) (   ) 10^-2

d) (   ) 10^-3

06) Simplifique a expressão

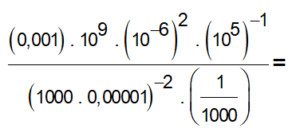
07) Simplifique a expressão e escreva o resultado em notação científica

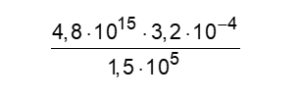
08) Determine as seguintes potências:

09) Determine os seguintes produtos, considerando que todos elementos do radicando sejam positivos:

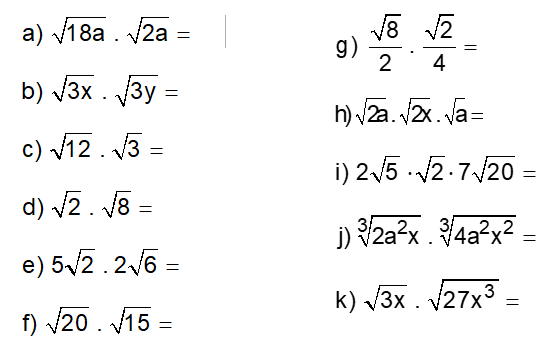
10) Racionalize os seguintes denominadores das frações algébricas, utilizando para isso o primeiro método:

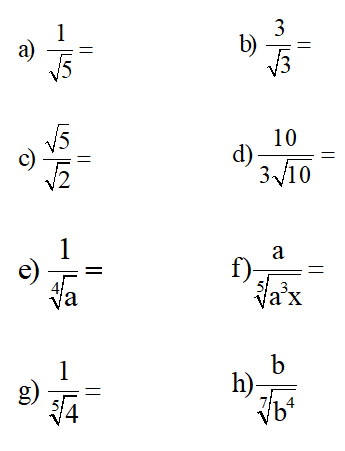
Você poderá imprimir essa atividade clicando no link!

8º MAT Atividade 1- Notação Cientifica -Potenciação e radiciação -Racionalização de denominadores