Potenciação e radiciação – Atividade 6 - 06/04/2021

POTENCIAÇÃO
Significa multiplicar um número real (base) por ele mesmo X vezes, onde X é a potência (número natural).
Exemplo:
32 (leia-se “três elevado ao quadrado”, ou “três elevado à segunda potência” ou ainda “três elevado à dois”).
No exemplo, precisamos multiplicar o 3 por ele mesmo. Ficando: 33 = 9.
Como consequência, temos que:
33 = 3 3
3 = 3
9 = 27.
34 = 3 3
3
3= 9
9 = 81.
Propriedades da Potenciação
P1 – Multiplicação de potências de bases iguais: Neste caso, mantem-se a base e somam-se os expoentes:
an am = an + m
Exemplo:
a) 52 ∙ 54 = 52 + 4 = 56 b) 23 ∙ 24 ∙ 22 = 23 + 4 +2 = 29
P2 – Divisão de potências de bases iguais: Nesta propriedade mantem-se a base e subtraem-se os expoentes:
(an) / (am) = an – m ,”a” diferente de zero.
Exemplo:
a) 312 34 = 312 – 4 = 38 b) 23
24 = 23 – 4 = 2–1
Observação: Temos que a1 = a, veja o exemplo:

Se m fosse igual a n teríamos am am = 1 ® a0 = 1ou seja, am – m = a0, portanto isso a0 = 1.
Exemplo:

P3 – Potência de potência: Nesta propriedade da potenciação temos que manter a base e multiplicar os expoentes.
(am)n = am . n
Exemplo:

P4 – Potenciação de números fracionários:
Na potenciação, quando elevamos um número fracionário a um determinado expoente, estamos elevando o numerador e o denominador a esse expoente, conforme os exemplos abaixo:
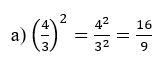
P5 – Multiplicação de bases diferentes elevadas ao mesmo expoente:
Neste caso efetua-se o produto das bases elevadas ao respectivo expoente.
(a ∙ b)n = an ∙ bn
Exemplo:

P6 – Divisão de bases diferentes elevadas ao mesmo expoente:
Neste caso efetua-se o quociente das bases elevadas ao respectivo expoente.
(a/b)n = an/bn , “b” diferente de zero.
Exemplo:

P7 – Potenciação com números negativos
1º caso: Com expoentes pares;
(-3)2 = 9, pois (-3)2 = (-3)∙(-3) = +9
-32 = -9 , pois –32 = -(3)∙(3) = – 9
Base negativa elevada a um expoente par, o resultado torna-se positivo. Note que, neste caso o sinal ‘– ‘está dentro dos parênteses e, portanto, também fica elevado ao expoente par. Caso contrário (no exemplo de baixo), o sinal negativo não está elevado, e portanto, ele continua no seu lugar no resultado.

2º caso: Com expoentes ímpares;
(-2)3 = – 8, pois (-2)3 = (-2) ∙ (-2) ∙ (-2) = – 8
-23 = (-1) ∙ 8, pois (-1)∙(2)3 = (-1) ∙ (2) ∙ (2) ∙ (2) = – 8
É importante observarmos que se o expoente é ímpar, o sinal da base permanece. Ou seja, o expoente ímpar conserva o sinal da base.
Veja outro exemplo:
a) (-3)3 = (-3) ∙ (-3) ∙ (-3) = 9 ∙ (-3) = -27 b) (7)3 = (7) ∙ (7) ∙ (7) = 343

Base elevada a expoente negativo: De forma simples, inverte-se a base e troca-se o sinal do expoente. Assim, se a base está no numerador da fração, ela passa para o denominador, se a base estiver no denominador, ela passará para o numerador, e nos dois casos, troca-se o sinal de expoente.
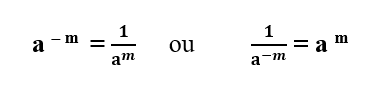
A recíproca é verdadeira. Demonstração:
a – m = a0 – m .
a – m = a0/am = 1/am .
Exemplo:

Notação científica
Alguns números ou medidas são expressos com muitos algarismos para indicar algo muito grande ou muito pequeno.
Para abreviar essa escrita de um número com muitos algarismos, podemos usar a notação científica.
Um número N escrito em notação científica apresenta-se da seguinte forma, com x ∈ ℚ:
N = x . 10n, com 1 ≤ | x | < 10
Exemplos:
* A distância da Terra à Lua é de, aproximadamente, 380 000 000 m. 3, 8 . 108 m
* O raio do átomo de hidrogênio é de aproximadamente 0,000 000 000 05 m. 5 . 10-11 m
ATIVIDADES
01. Transforme em produto ou quociente de potências.

02. Determine as seguintes potências:

03. Em cada uma das propriedades da potenciação descreva o método utilizado para seu respectivo desenvolvimento.
a) Multiplicação de potências de mesma base: _____________________________________________________________________________
_____________________________________________________________________________________________________________________________
b) Divisão de potências de mesma base: __________________________________________________________________________________
_____________________________________________________________________________________________________________________________
c) Potência de potência: ___________________________________________________________________________________________________
_____________________________________________________________________________________________________________________________
d) Multiplicação de bases diferente elevadas ao mesmo expoente: _______________________________________________________
______________________________________________________________________________________________________________________________
e) Divisão de bases diferente elevadas ao mesmo expoente: ______________________________________________________________
______________________________________________________________________________________________________________________________
04. Aplicando as propriedades das potências de mesma base, reduza a uma só potência as seguintes expressões:
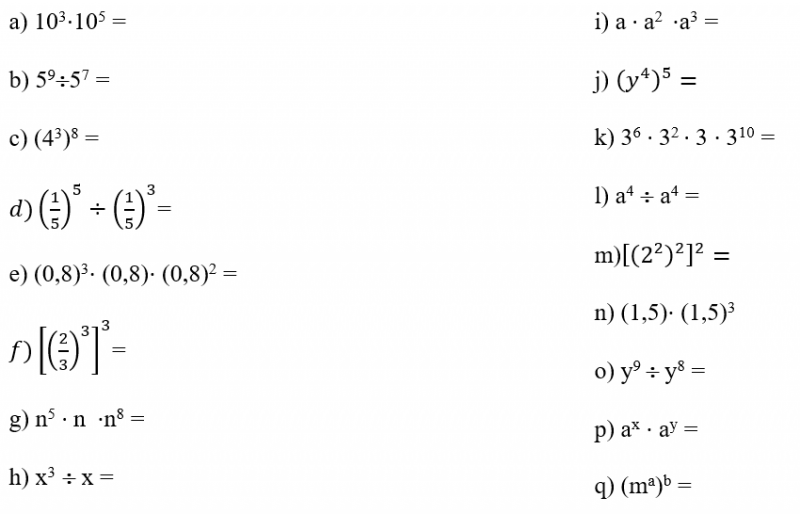
05. Escreva cada número na forma de notação científica.
a) 5 000
b) 3 210 000
c) 7 850 000 000
d) 0,002
e) 0,000 003 24
f) 0,000 000 012 3
06. Um famoso físico escreveu para uma revista científica afirmando que “átomos têm diâmetros de aproximadamente um décimo de bilionésimo de metro”. A representação dessa medida em notação científica é:
a) ( ) 1 . 10-8 m
b) ( ) 1 . 10-9 m
c) ( ) 1 . 10-10 m
d) ( ) 1 . 10-11 m
ESTUDO DA RADICIAÇÃO
Definição: Dados um número natural n ( com n 2 ), chama-se raiz n-ézima de a o número real b, tal que:




08.Aplicando a propriedade, complete as igualdades:

09.Transforme num quociente de radicais:

10.Aplicando a propriedade, reduza a um só radical:

11.Dividindo o índice do radical e o expoente do radicando pelo m.d.c entre eles, complete as igualdades:

12.Racionalize os denominadores abaixo:

NÃO ESQUEÇA DE IMPRIMIR SUA ATIVIDADE!!!
