Potenciação e radiciação. Notação Científica – Atividade 10 - 02/06/2021
POTENCIAÇÃO
Potenciação significa multiplicar um número real (base) por ele mesmo X vezes, onde X é a potência (número natural).
Exemplo:
32 (leia-se “três elevado ao quadrado”, ou “três elevado à segunda potência” ou ainda “três elevado à dois”).
No exemplo, precisamos multiplicar o 3 por ele mesmo. Ficando: 3 x 3 = 9
Como consequência, temos que:
33 = 3 x 3 x 3 = 3 x 9 = 27
34 = 3 x 3 x 3 x 3= 9 x 9 = 81
Propriedades da Potenciação
P1 – Multiplicação de potências de bases iguais: Neste caso, mantém-se a base e somam-se os expoentes:
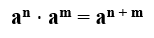
Exemplo:

P2 – Divisão de potências de bases iguais: Nesta propriedade mantem-se a base e subtraem-se os expoentes:
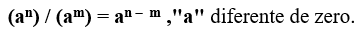
Exemplo:

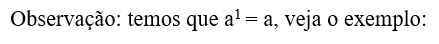
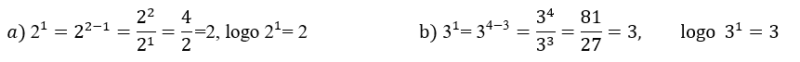
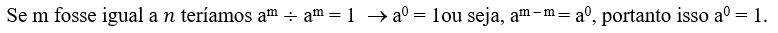
Exemplo:

P3 – Potência de potência: Nesta propriedade da potenciação temos que manter a base e multiplicar os expoentes.
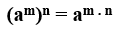
Exemplo:

P4 – Potenciação de números fracionários: Quando elevamos um número fracionário a um determinado expoente, estamos elevando o numerador e o denominador a esse expoente, conforme os exemplos a seguir:
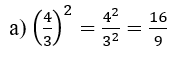
P5 – Multiplicação de bases diferentes elevadas ao mesmo expoente: Neste caso efetua-se o produto das bases elevadas ao respectivo expoente.
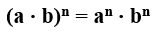
Exemplo:

P6 – Divisão de bases diferentes elevadas ao mesmo expoente: Neste caso efetua-se o quociente das bases elevadas ao respectivo expoente.
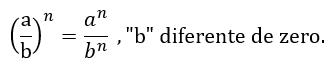
Exemplo:

P7 – Potenciação com números negativos
1º caso: Com expoentes pares
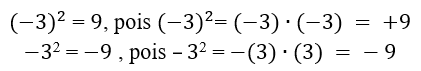
Base negativa elevada a um expoente par, o resultado é positivo. Note que, neste caso o sinal ‘– ‘está dentro dos parênteses e, portanto, também fica elevado ao expoente par. Se o sinal não está dentro do parêntese, ele não será elevado ao expoente.

2º caso: Com expoentes ímpares
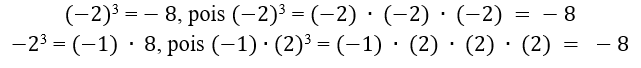
É importante observarmos que se o expoente é ímpar, o sinal da base permanece. Ou seja, o expoente ímpar conserva o sinal da base.
Veja outro exemplo:
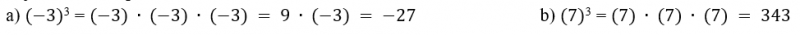

Base elevada a expoente negativo: Neste caso, inverte-se a base e troca-se o sinal do expoente. Assim, se a base está no numerador da fração, ela passa para o denominador, se a base estiver no denominador, ela passará para o numerador, e nos dois casos, troca-se o sinal de expoente.
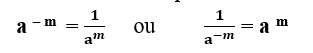
A recíproca é verdadeira. Demonstração:
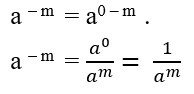
Exemplo:

ATIVIDADES
01. Transforme em produto ou quociente de potências.

02. Determine as seguintes potências:

03. Efetuar as operações indicando o resultado em forma de potência:

04.
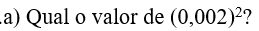
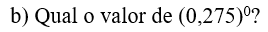
05. Em cada uma das propriedades da potenciação descreva o método utilizado para seu respectivo desenvolvimento.
a) Multiplicação de potências de mesma base: __________________________________________________ _______________________________________________________________________________________
b) Divisão de potências de mesma base: ______________________________________________________
_______________________________________________________________________________________
c) Potência de potência: ___________________________________________________________________
_______________________________________________________________________________________
d) Multiplicação de bases diferente elevadas ao mesmo expoente: __________________________________
_______________________________________________________________________________________
e) Divisão de bases diferente elevadas ao mesmo expoente: _______________________________________
_______________________________________________________________________________________
06. Aplicando as propriedades das potências de mesma base, reduza a uma só potência as seguintes expressões:
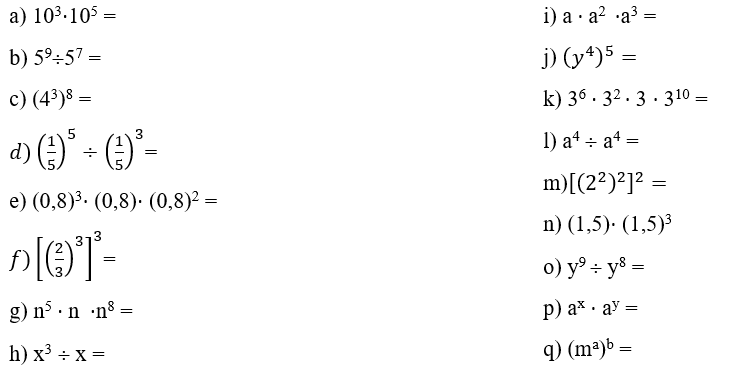
07. Determine o valor das seguintes expressões numéricas:

Notação Científica
A notação científica é uma forma padronizada de escrever números às vezes muito grandes ou muito pequenos usando potência de 10. Sua aplicabilidade para reduzir a escrita de números que apresentam muitos algarismos facilitam cálculos e formas de expressar resultados, padronizando as formas de apresentação numéricas.
O campo da Física e da Química utilizam largamente a notação científica para expressar resultados que teriam um número muito grande de algarismos.
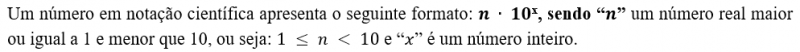
Exemplos
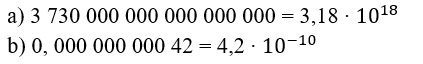
Transformar um número em notação científica
Veja a seguir como transformar os números em notação científica de forma prática:
1º Passo: Escrever o número na forma decimal;
2º Passo: Reescrever o número na forma decimal com apenas um algarismo diferente de 0 na frente da vírgula.
3º Passo: Colocar no expoente da potência de 10 o número de casas decimais que tivemos que deslocar com a vírgula. É importante observar que:
- Se o deslocamento da vírgula for para esquerda fazendo com que o valor do número diminua, o expoente ficará positivo;
- Se o deslocamento da vírgula for para direita fazendo com que o valor do número aumente, o expoente ficará negativo;
4º Passo: Escrever o produto do número pela potência de 10.
Veja alguns exemplos:

ATIVIDADES
08) Escreva os números a seguir em notação científica.

ESTUDO DA RADICIAÇÃO
Definição: Dados um número natural n (com n 2), chama-se raiz n-ézima de a o número real b, tal que:
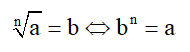

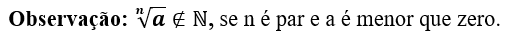
Exemplo:

Propriedades
1 – Multiplicação de radicais de mesmo índice: Conserva-se o índice e multiplica-se os radicandos.
Exemplo:

2 – Divisão de radicais de mesmo índice: Conserva-se o índice e dividem-se os radicandos.
Exemplo:

3 – Radical de um radical: Conserva-se o radicando e multiplica-se os índices.
Exemplo:

4 – Radicais equivalentes: Quando se multiplica ou se divide o índice do radical e o expoente do radicando por um mesmo número real diferente de zero, obtém-se um radical equivalente.
Exemplo:

RACIONALIZAÇÃO DE DENOMINADORES DO TIPO
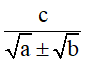
Temos o seguinte método:
I – Multiplica-se o numerador e o denominador pelo conjugado do denominador, a fim de se obter no denominador o produto da soma pela diferença de dois termos.
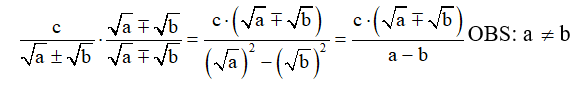
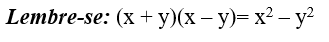
ATIVIDADES
09. Transforme num produto de radicais.

10. Aplicando a propriedade, complete as igualdades.

11. Transforme num quociente de radicais.


12. Aplicando a propriedade, reduza a um só radical.

13. Simplifique os radicais.

14. Racionalize os denominadores a seguir.

Se for possível, clique aqui para baixar e imprimir sua aula.
