Princípio multiplicativo da contagem – Atividade 6 - 06/04/2021

Estudo dos métodos de contagem (Princípio Fundamental Da Contagem).
A parte da matemática que estuda o número de possibilidades de um evento ocorrer é denominada de Análise Combinatória. Em uma linguagem simplificada, a Análise Combinatória é a arte de contar. Nem sempre contar é um processo simples. Por exemplo:
No sorteio da Mega Sena são sorteadas 6 dezenas escolhidas entre os números inteiros 1 e 60. De quantas formas distintas pode-se fazer essa escolha?
Logo de início podemos perceber que existe um número muito grande de possibilidades para montarmos um jogo em uma cartela e que é necessária certa técnica para determinarmos quantas possibilidades existem.
Entendemos, portanto, que para calcular a quantidade de possibilidades de ocorrência de um determinado acontecimento usamos os métodos de contagem da Análise Combinatória. É importante notar que muitas vezes não teremos que representar todas as possibilidades de um experimento, dados que essa quantidade seria muito grande o que tornaria a tarefa difícil e cansativa. Na maioria das vezes só teremos que contar essas possibilidades. No entanto, a técnica que permite a descrição das possibilidades de um experimento é chamada de Diagrama ou Árvore de Possibilidades.
Árvore ou Diagrama de possibilidades:
É um esquema que nos permite a visualização de todas as possibilidades de um acontecimento, a partir de um diagrama que se ramifica de acordo com as possibilidades do evento considerado. Para melhor explicar esta técnica vamos nos apoiar em um exemplo.
Exemplo 01. Uma moeda é lançada 3 vezes. Qual o número de sequências possíveis para cara ou coroa?
Solução: Note que no primeiro lançamento existem duas possibilidades: pode sair cara (K) ou pode sair coroa (C);
Já no segundo lançamento, existem quatro sequências possíveis. São essas: {(K,K);(K,C);(C,K);(C,C)};
Ao considerarmos o terceiro lançamento, existem agora oito sequências possíveis, que são: {(K,K,K); (K,K,C); (K,C,K); (K,C,C); (C,K,K); (C,K,C); (C,C,K); (C,C,C)}. Pelo diagrama teremos:
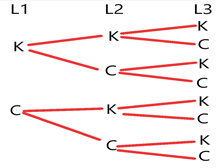
Portanto temos oito sequências possíveis.
É importando notar que, se trocarmos a moeda por um dado com seis faces, e considerarmos os mesmos lançamentos teremos um número de possibilidades extremamente maior, pois para o primeiro lançamento teríamos seis possibilidades. No segundo lançamentos, para cada uma das seis primeiras ramificações, teríamos outras seis ramificações, e assim por diante, até o último lançamento.
Exemplo 02. Para ir ao clube, Júnior deseja usar uma camiseta, uma bermuda e um par de tênis. Sabendo que ele dispõe de 4 camisetas, 2 bermudas e 3 pares de tênis, de quantas maneiras distintas poderá vestir-se?
Solução: Note que na primeira escolha Júnior disponha de 4 camisetas {C1, C2, C3, C4}. Já na segunda escolha, da bermuda, dispunha de 2 possibilidades {B1, B2} e, para a terceira escolha, possui 3 pares de tênis {T1, T2, T3}, assim nosso diagrama será:
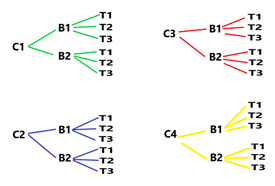
Portanto nestas condições, Júnior terá 24 possibilidades para se vestir.
Princípio Fundamental da Contagem
Se um acontecimento ocorrer em “n” etapas distintas e independentes entre si, A = {E1, E2, E3, E4, … , En}, então o número total de possibilidades deste acontecimento ocorrer P(A) obtido fazendo-se o produto entre o número de possibilidades de ocorrência de cada etapa, ou seja, é:
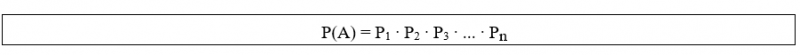
Onde:
- P1 é o número de possibilidades da 1ª etapa (E1);
- P2 é o número de possibilidades da 2ª etapa (E2);
- P3 é o número de possibilidades da 3ª etapa (E3);
- Pn é o número de possibilidades da n-ésima etapa (En);
Exemplo 3. Uma moeda é lançada 3 vezes. Qual o número de sequências possíveis para cara ou coroa?
Solução: Note que no primeiro lançamento existem duas possibilidades: pode sair cara (K) ou pode sair coroa (C) e P(L) o número de possibilidades do lançamento, teremos, pelo Princípio Fundamental da Contagem:
Total de possibilidades = P(L1) x P(L2) x P(L3) = 2 x 2 x 2 = 8 possibilidades.
Note que por essa técnica, não existe a preocupação em descrever cada possibilidade, e sim só contamos o total de possibilidades.
Nestas condições, aplicando o mesmo critério, podemos contar quantas possibilidades de resultados podem ser obtidas se, ao invés de uma moeda, tivéssemos utilizado um dado. Assim teremos:
Total de possibilidades = P(L1) x P(L2) x P(L3) = 6 x 6 x 6 = 216 possibilidades.
Exemplo 4. Para ir ao clube, Júnior deseja usar uma camiseta, uma bermuda e um par de tênis. Sabendo que ele dispõe de 4 camisetas, 2 bermudas e 3 pares de tênis, de quantas maneiras distintas poderá vestir-se?
Solução: Número de possibilidades para se vestir P(V) depende do número de possibilidades de cada etapa:
a) 1ª Etapa: Escolha da camiseta = 4;
b) 2ª Etapa Escolha da bermuda = 2;
c) 3ª Etapa Escolha do tênis = 3,
P(V) = P(C) ∙ P(B) ∙ P(T) = 4 ∙ 2 ∙ 3 = 24 possibilidades.
Nestas condições, Júnior possui 24 maneiras distintas para se vestir.
Exemplo 5. As atuais placas de licenciamento de automóveis constam de sete símbolos (caracteres) sendo três letras, dentre as 26 do alfabeto, seguidas de quatro algarismos. Quantas placas distintas podem ter sem a repetição de letras ou de algarismos, ou seja, com todos os caracteres distintos?
Solução: Neste caso perceba que cada caractere da placa possui uma quantidade de escolhas possíveis.
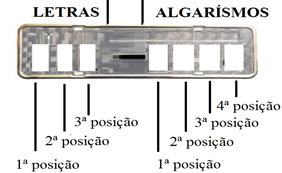
Para a 1ª letra: 26 possibilidades de escolha;
Para a 2ª letra: 25 possibilidades de escolha, uma vez que uma letra já foi escolhida;
Para a 3ª letra: 24 possibilidades de escolha, pois agora, duas letras já foram escolhidas.
Para o 1º algarismo: 10 possibilidades de escolha.
Para o 2º algarismo: 9 possibilidades de escolha, pois um algarismo já foi usado;
Para o 3º algarismo: 8 possibilidades de escolha; pois dois algarismos já foram usados;
Para o 4º algarismo: 7 possibilidades de escolha. pois três algarismos já foram usados.
Portanto, pelo Princípio Fundamental da Contagem:
No de Placas = 26 x 25 x 24 x 10 x 9 x 8 x 7 = 78.624.000 placas possíveis.
Nestas condições, o número de placas possíveis é 78.624.000.
ATIVIDADES
01) Lívia quer pintar as quatro paredes de seu quarto de modo que paredes adjacentes tenham cores distintas e ainda não sejam repetidas as cores. Ela dispõe de cinco tipos de cores e considera que todas as paredes são diferentes. De quantas maneiras diferentes Lívia pode pintar seu quarto?
A) ( ) 24 maneiras.
B) ( ) 48 maneiras.
C) ( ) 60 maneiras.
D) ( ) 120 maneiras.
02) Um restaurante oferece, 3 opções de carne e 5 de saladas no prato feito (PF). Um cliente só pode escolher um tipo de carne e um tipo de salada. Nestas condições, de quantas maneiras distintos um cliente pode montar sua refeição, sabendo que ele colocar uma carne e uma salada?
A) ( ) 2 maneiras.
B) ( ) 8 maneiras.
C) ( ) 10 maneiras.
D) ( ) 15 maneiras
03) No esquema adiante, suponha que os países A, B e C possuem uma logística do transporte de mercadorias com o menor custo/tempo.
Os números indicados representam o número de rotas distintas de transportes disponíveis, nos sentidos indicados. Por exemplo, de A até B são 5 rotas.
Nessas condições, o número total de rotas distintas, de A até C é igual a
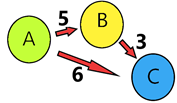
A) ( ) 6.
B) ( ) 8.
C) ( ) 14.
D) ( ) 21.
04) Um auditório de uma escola da rede estadual dispõe de 6 portas, que podem ser utilizadas tanto como entrada ou para saída. De quantos modos distintos um aluno que se encontra fora do auditório pode entrar e sair do mesmo, utilizando como porta de saída uma porta diferente da que utilizou para entrar?
A) ( ) 36.
B) ( ) 30
C) ( )11.
D) ( ) 6.
05) No vestiário de um ginásio em uma escola da rede estadual há exatamente 30 armários, cada qual para uso individual. No dia que ocorreu uma competição, dois alunos dessa escola foram utilizar o vestiário para se mudar suas roupas e colocarem seus uniformes, apenas, dos armários estavam desocupados.
Quantas opções eles terão para escolher seus respectivos armários?
A) ( ) 56.
B) ( ) 46.
C) ( ) 36.
D) ( ) 26.
06) Com o objetivo de melhorar o transporte público, o governo do estado propôs a construção de três terminais de ônibus, em uma de suas cidades. Para estabelecer conexão entre os terminais, foram estipuladas as seguintes quantidades de linhas de ônibus:
– do terminal A para o B 5 linhas distintas;
– do terminal B para o C 7 linhas distintas;
Supondo que um passageiro utilize exatamente duas linhas de ônibus para ir do terminal para o terminal calcule a quantidade possível de trajetos distintos que ele poderá fazer.
07) Um palíndromo ou capícua é um número, que se lê da mesma maneira nos dois sentidos, ou seja, da esquerda para a direita ou ao contrário, como 333, 1661 e 28482.
Nestas condições, determine à quantidade de palíndromos que podem sem escrito, com cinco algarismos distintos, do nosso sistema de numérico.
08) Um ano após o início da pandemia, o cinema prometer vir com força total. Grandes filmes da Marvel, DC Comics, e outros grande estúdio são promessas para esse ano, tais como:
VIÚVA NEGRA;
007 – SEM TEMPO PARA MORRER;
OS ETERNOS
O ESQUADRÃO SUICIDA
HOMEM-ARANHA 3
GODZILLA VS KONG
RAYA E O ÚLTIMO DRAGÃO

MATRIX 4
Em uma escola da rede estadual, os três alunos João, Pedro e Lorraine, com a média mais alta ganharam um ingresso cada para o cinema. No entanto, a escola só tem um ingresso de cada um dos filmes listados acima. Nestas condições, de quantas sequências distintas os ingressos podem ser escolhidos, sabendo que a escolha é feita de aluno por aluno?
09) Numa lanchonete o lanche é composto por três partes: pão, molho e recheio. Se essa lanchonete oferece aos seus clientes duas opções de pão, três de molho e quatro de recheio, a quantidade de lanches distintos que ela pode oferecer é de
A) ( ) 9
B) ( ) 12
C) ( ) 18
D) ( ) 24
10) Renata vai colocar uma senha de 4 dígitos distintos no celular, ou seja, sem dígitos repetidos. Ela quer utilizar os algarismos 6, 7, 8 e 9. Quantas senhas diferentes Renata pode criar?
SE POSSÍVEL, VOCÊ PODE BAIXAR E IMPRIMIR SUA ATIVIDADE!!!
