Fala galera! Vamos aprender hoje sobre Radiciação

Radiciação é a operação que realizamos quando queremos descobrir qual o número que multiplicado por ele mesmo, uma determinada quantidades de vezes, dá um valor que conhecemos.

Veja o vídeo a seguir explicando melhor sobre o assunto.

Exemplo

Qual é o número que multiplicado por ele mesmo 3 vezes dá como resultado 125?

Por tentativa podemos descobrir que:

5 x 5 x 5 = 125

Logo, o 5 é o número que estamos procurando.

Definição

Seja a um número real não negativo e n um número natural, com n ≥ 1,  chamamos de raiz enésima de a se, e somente se, o número real x, não negativo, elevado ao expoente n, resulta em a. Vamos entender um pouco melhor essa definição. Para representarmos radicais utilizamos o símbolo √, chamado de radical. Onde n é o índice da raiz, a é o radicando e b a raiz. Leia-se: raiz enésima de a é igual a b.

Vamos fazer alguns exemplos.

Relação entre potência e raiz

Toda potência de base positiva e expoente racional é uma raiz, descrita da seguinte forma:

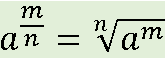
O denominador n é o índice da raiz e o numerador m é o expoente do radicando.

Propriedades

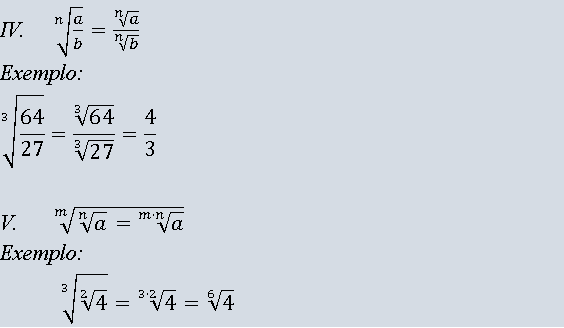
Simplificação de radicais.

Quando dizemos que um número está na forma simplificada, queremos mostrar que há uma maneira mais simples, de interpretá-lo. As raízes exatas já são representadas de uma forma simples. Vamos ver esse processo de simplificação por meio de exemplos.

Operações com radicais

Vamos estudar as operações de adição, subtração, multiplicação e divisão com radicais a relação entre potenciação e radiciação.

Adição e subtração com radicais

Utilizaremos o mesmo conceito de soma algébrica de polinômios, colocando a parte literal(raiz) em evidência e somando os coeficientes.

Exemplos:

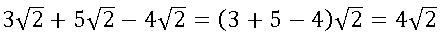
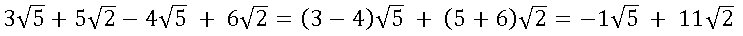
Observe o seguinte exemplo.

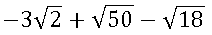
Aparentemente, as raízes não são semelhantes. Contudo, algumas raízes podem ser escritas de forma simplificada.

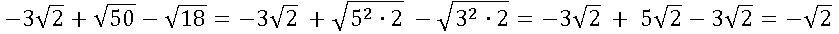
Aplicação

Carlos estava estudando o conceito de perímetro de uma figura plana. Ele estava resolvendo alguns exercícios, entre eles estava o seguinte:

“Calcule o perímetro de um retângulo ABCD de √75 cm de comprimento e √20 cm de largura.”

Como Carlos resolveu esse problema?
Vamos desenhar o problema e identificar as informações no desenho:

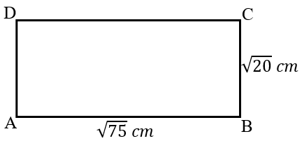
Perceba que o lado AB = CD = √75 cm e BC = AD = √20 cm.

Note também que √75=√(5^2∙5)=5√5 e √20=√(2^2∙5)=2√5.

Para calcular o perímetro, devemos somar todos os lados do retângulo.

Perímetro = AB + BC + CD + DA = 5√5 +2√5 +5√5 +2√5 = 14√5 cm

Multiplicação e divisão com radicais

A multiplicação das raízes de mesmo índice é igual à raiz do produto, nesse indica.

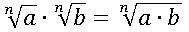
Exemplos:

A divisão das raízes de mesmo índice é igual à raiz do quociente, nesse indica.

Aplicação:

Carlos estava estudando o conceito de perímetro de uma figura plana. Ele estava resolvendo alguns exercícios, entre eles estava o seguinte
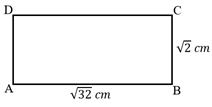
“Calcule a área de um retângulo ABCD de √32 cm de comprimento e √2 cm de largura.”
Vamos desenhar o problema e identificar as informações no desenho.

A área de um retângulo é dada por:

Área = comprimento ∙ largura
Calculando a área do retângulo ABCD
Área = comprimento ∙ largura
Área = √32 ∙ √2
Área = √64
Área = 8 cm²

Agora pratique resolvendo os seguintes exercícios no caderno.

01. Associe os valores da coluna (I), com suas respectivas raízes na coluna (II).

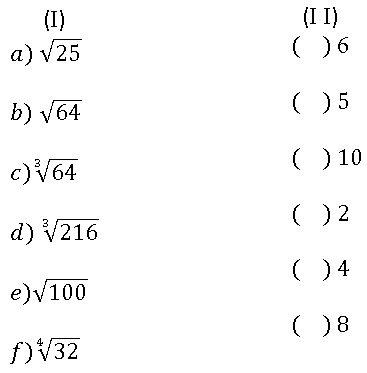
02. Indique se a sentença é verdadeira ou falsa.

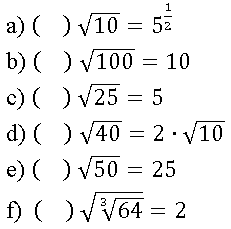
03. Simplifique, utilizando as propriedades dos radicais.

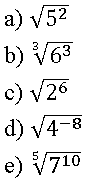
04. Simplificando-se 2√3 + 2√12 – 2√75 obtém-se:

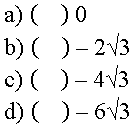
05. Encontre o valor de x para a expressão: √8 + √64 – 5√2 = x.

06. Simplifique a expressão a seguir:

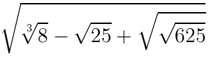
07. Calcule o perímetro de um retângulo ABCD de √108 cm de comprimento e √27 cm de largura.

08. Calcule a área de um retângulo ABCD de √50 cm de comprimento e √8 cm de largura.

Ufa!! Acabamos por aqui!

Lembrem-se de compartilhar essa atividade com seus colegas e com o seu professor.

Até a próxima, pessoal!!!