Vamos começar nossa atividade!!!

Estudo de Transformações Geométricas

         Transformação geométrica é uma aplicação objetiva entre duas figuras geométricas, no mesmo plano ou em planos diferentes, de forma que, a partir de uma figura geométrica original, forma-se outra figura geometricamente igual ou equivalente. Uma transformação geométrica é, portanto, uma correspondência, um a um, entre pontos de um mesmo plano ou de planos diferentes.

       Congruência: Dizemos que duas figuras são congruentes quando sobrepostas, percebe-se que são perfeitamente iguais. Neste caso temos uma correspondência entre as medidas dos lados e ângulos e a manutenção da forma e do tamanho.

Exemplo:

Maria construiu o triângulo de vértices em ABC e João construiu o triângulo de vértices em DEF, como mostra a figura a seguir.

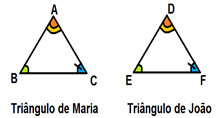
       Perceba que os triângulos são semelhantes. Eles possuem lados de mesmas medidas e ângulos internos de medidas iguais, porém não são os mesmos triângulos.

      Figuras congruentes fazem parte de uma rede chamada transformações isométricas (ou simetrias), que por sua vez é dividida em três naturezas (reflexão ou simetria, translação e rotação):

       Reflexão ou Simetria: Como o próprio nome sugere, trata-se do reflexo da figura como a de um espelho, ou seja, verifica-se o espelhamento de uma figura em relação a um eixo, que é denominado eixo de simetria. Esse eixo divide um plano em dois semi-planos, separando uma imagem original de seu reflexo, conservando a forma, o ângulo e o tamanho – deixando uma invertida em relação à outra.

        As figuras refletidas têm um ponto correspondente ao outro em cada lado do eixo e mantêm a distância em relação ao eixo de simetria.

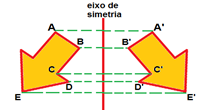
       Translação: transladar uma figura pode ser entendido, de forma simplificada como sendo “carregar” ou transportar  a figura para outro lugar, mantendo suas características como tamanho dos lados, ângulos internos e direção. Neste caso a diferença entre as figuras está simplesmente em suas posições em relação a um referencial.

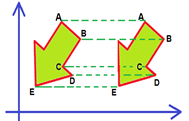
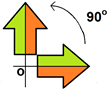
•           Rotação: Nessa transformação, tomado um ponto de rotação, qualquer segmento que parta do ponto de rotação e chegue em um ponto da figura sobre uma rotação segundo um ângulo escolhido. Quanto mais afastado do centro de rotação, mais aparente será do deslocamento desse ponto.

         Neste exemplo, para rotacionar a figura em 90° no sentido anti-horário, tomamos como centro de rotação o ponto “O” que deve ser o ponto de partida para medir o ângulo determinado, e assim a seta que antes apontava para a direita, foi rotacionada 90º e agora, transportada, aponta para cima. Essa transformação mostra como resultado imagens congruentes “iguais”, com os ângulos e os lados correspondentes medindo o mesmo valor  a partir do centro.

Atividades

1) Observe a figura a seguir.

Assina a alternativa que indica a imagem refletida dessa figura segundo o eixo de simetria.

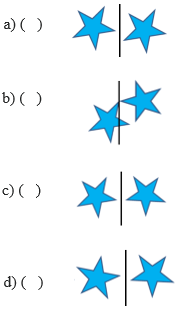
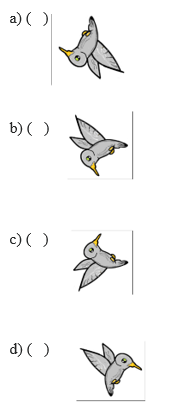
2. Observe a figura a seguir.

Considere que a imagem será rotacionada 180º no sentido anti-horário e depois, terá suma imagem refletida para a direita. Nestas condições, a imagem final será:

3) Observe as figuras a seguir.

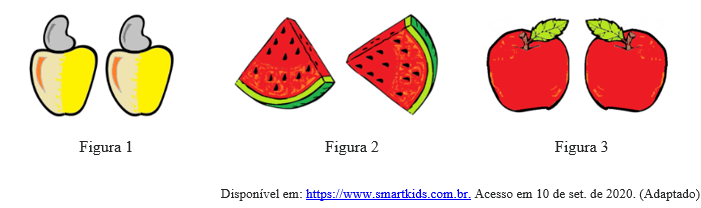
Considerendo as figuras 1, 2 e 3 podemos dizer que as transformações isoformicas ocorridas foram:

a) (   ) Rotação, Translação e Reflexão.

b) (   ) Translação, Reflexão e Rotação.

c) (   ) Translação, Rotação e Reflexão.

d) (   ) Reflexão, Rotação e Translação.

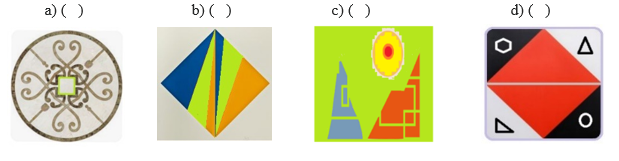
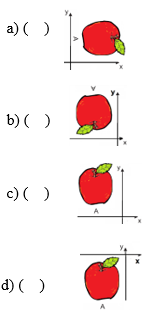
4) Figuras com alguma simetria estão constantemente aparecendo ao nosso redor. Elas podem ser percebidas no espelho, em algumas flores, em uma toalha de mesa. Sabemos que duas figuras são simétricas quando existe um espelho entre elas e todos os pontos simétricos estão equidistantes ao espelho. Nestas condições, a figura que se encaixa na descrição acima é:

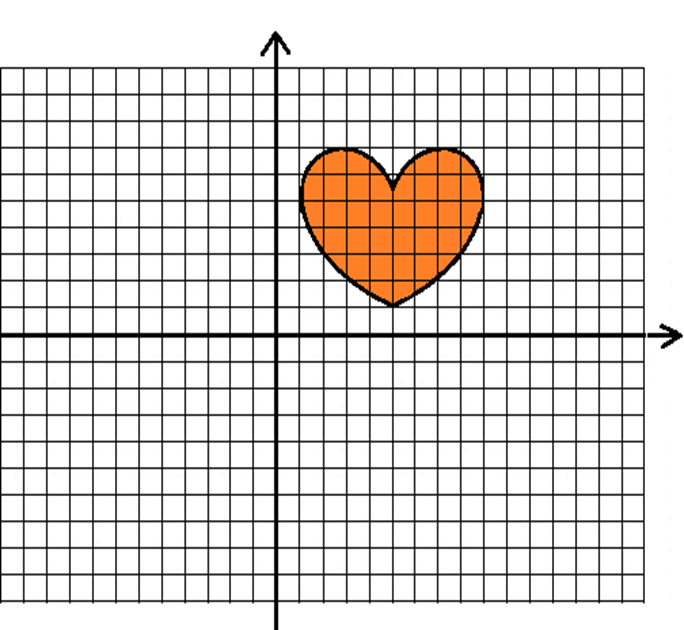
5) Observe a figura na malha quadriculada a seguir. Desenhe no quadrante correspondente a reflexão dessa figura em relação aos eixos coordenados.

6)  Veja a figura a seguir.

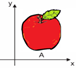
Essa figura sofreu cinco transformações isométricas, nessa ordem:

1ª) Reflexão no eixo

2ª) Rotação de 90º  graus no sentido anti-horário, com centro de rotação na origem do plano cartesiano;

Nestas condições, qual será a posição final?

Qual a posição final da figura?

7) Em um círculo recortado em papel cartão foi colocado o desenho do mestre renascentista Leonardo Da Vinci, O Homem Vitruviano. Esse círculo foi utilizado para montar uma roleta, conforme a figura 1 a seguir, fixada em uma parede. Quando a roleta é acionada, o círculo gira livremente em torno do seu centro, e o triângulo indicador permanece fixo na parede.

Considerando, inicialmente, a imagem da tela do mestre renascentista, na posição da figura 1, obtém-se, após a roleta realizar uma rotação de três quartos de volta, no sentido anti-horário, a figura 

8) Dizemos que uma imagem tem alguma simetria se, de uma maneira simples, ela puder ser dobrada ao meio e as partes se sobreporem de forma perfeita. Assim, dentre os símbolos abaixo, qual é simétrico e qual não é?

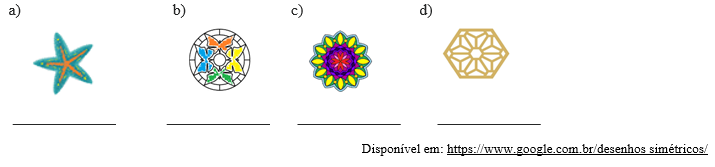
9) Existe um tipo de simetria que é observada em alguns seres vivos, como os equinodermos. É uma espécie de simentria circular ela é chamada de simetria radial. Dê acordo com o número de repetições (pontas) ela pode ser:

Triradial      →   com três pontas;

Tetraradial  →   com quatro pontas;

Pentaradial    →   com cinco pontas;

Dê acordo com o texto acima, classifique as simetrias radiais dos objetos abaixo:

Concluímos!!! Vamos revisar!!!

Baixe e imprima sua atividade!