Demonstrações de relações entre os ângulos formados por retas paralelas intersectadas por uma transversal – Atividade 8 - 06/05/2021
ÂNGULOS FORMADOS POR DUAS RETAS PARALELAS CORTADA POR UMA
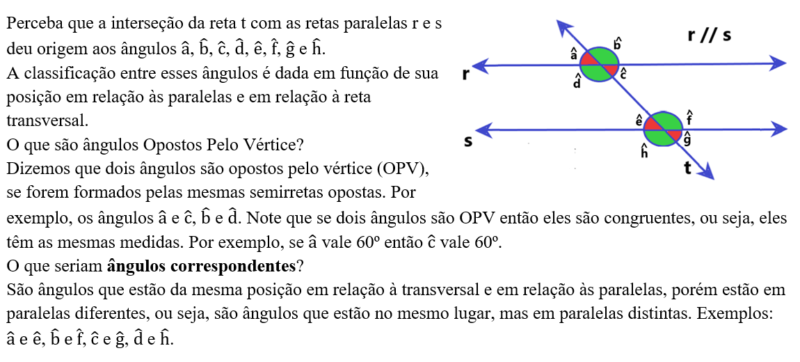
Podemos dizer que se dois ângulos são correspondentes então eles são congruentes, ou seja, eles têm as mesmas medidas. Ou seja, por exemplo: Se mede 60º então
também mede 120º, Se
mede 120º então
, também mede 120º.
Com relação às paralelas, o que significa dizer que os ângulos são internos ou externos?
Se eles estiverem entre as retas paralelas, dizemos que esses ângulos são internos; se não estiverem entre as paralelas dizemos que eles são externos.
Em relação à transversal, o que significa dizer que dois ângulos são colaterais?
Os elementos colaterais são aqueles que estão do mesmo lado. Pois bem, se dois ângulos são colaterais então eles estão do mesmo lado em relação à transversal, ou seja, ou os dois ângulos estão à direita ou à esquerda da transversal.
Por conseguinte, se estiverem de lados opostos ou alternados em relação à transversal dizemos que esses ângulos são alternos.
Perceba então que podemos classificar os pares de ângulos de quatro formas:
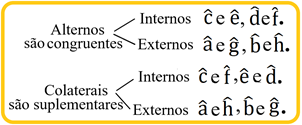
Observe que se dois ângulos são alternos, sejam internos ou externos, eles são congruentes, isto é, possuem as mesmas medidas. Por outro lado, se dois ângulos forem colaterais, sejam internos ou externos, eles são suplementares, isto é, sua soma é 180o.
TEOREMA DE TALES
TEOREMA; “Se um feixe de retas paralelas for interceptado por retas transversais então se formam segmentos correspondentes que são proporcionais.”
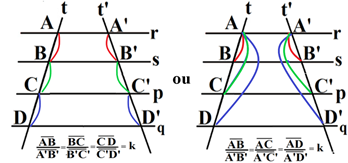

RELAÇÕES MÉTRICAS NO ∆ RETÂNGULO
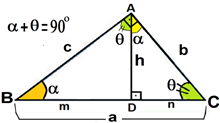
Os elementos de um triângulo retângulo estão apresentados a seguir:
Sendo:
a: medida da hipotenusa (lado oposto ao ângulo de 90º)
b: cateto
c: cateto
h: altura relativa à hipotenusa
m: projeção do cateto c sobre a hipotenusa
n: projeção do cateto b sobre a hipotenusa
SEMELHANÇA E RELAÇÕES MÉTRICAS
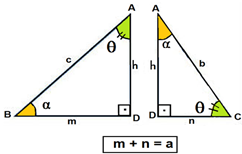
Considere os triângulos semelhantes ABC, DBA e DAC, representados nas imagens:

TEOREMA DE PITÁGORAS
Temos ainda que a soma das projeções m e n é igual a hipotenusa, ou seja: m + n = a.
A mais importante das relações métricas é o Teorema de Pitágoras. Podemos demonstrar o teorema usando a soma de duas relações encontradas anteriormente.
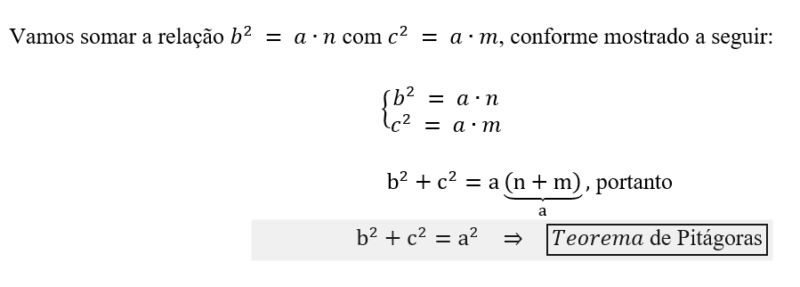
ATIVIDADES
01) Calcule x, sabendo que r//s:
a)
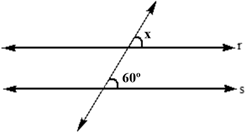
b)
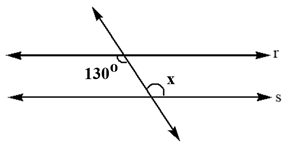
c)
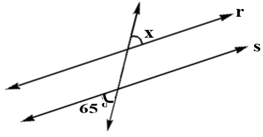
d)
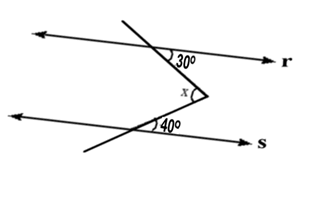
e)
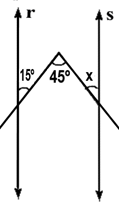
f)
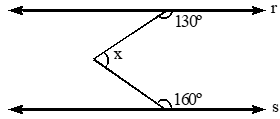
02) Sendo as retas r e s paralelas, determine o valor do ângulo Â.
A) ( ) 111º .
B) ( ) 112º.
C) ( ) 113º. D) ( ) 114º.
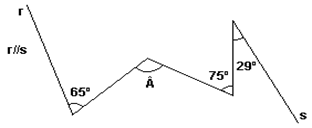
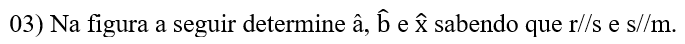
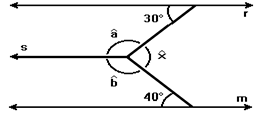
04) Sabendo que as retas a, b e c são retas paralelas, utilize o Teorema de Tales e determine o valor de x na figura a seguir:
a)
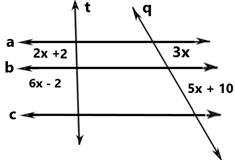
b)
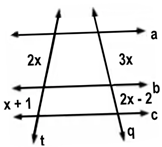
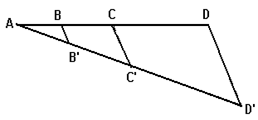
06) A seguir estão duas retas paralelas cortadas por duas transversais. Calcule o valor de x.
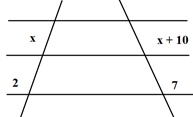
07) Determine x e y nos casos:
a)
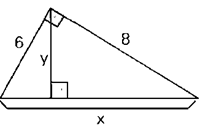
b)
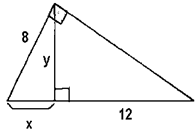
08) Determine o valor de x nos casos:
a)
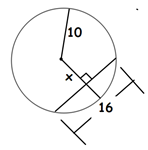
b)
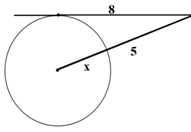
09) Observe o triângulo retângulo ABC a seguir.
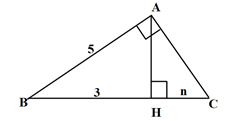
Sabendo que o ângulo A é reto, o valor de n é
A) ( ) 22/3
B) ( ) 16/3
C) ( ) 22
D) ( ) 16
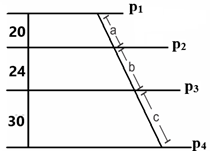
10) Na figura a seguir, as retas p1, p2, p3 e p4 são paralelas e, a, b e c representam medidas dos segmentos tais que a + b + c = 111. Conforme esses dados, os valores de a,b e csão, respectivamente, iguais a
A) ( ) 30, 36 e 45.
B) ( ) 20, 26 e 35.
C) ( ) 30, 36 e 44.
D) ( ) 60, 27 e 88.
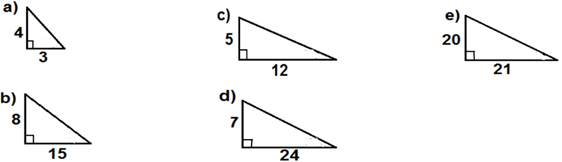
11) Determine as medidas das hipotenusas nos triângulos retângulos a seguir: