Aula 3 – Matemática 6º Ano - 22/04/2020
Oi galera!! Você conhece
Hoje vamos conhecer a decomposição de números com números primos para se chegar no MMC e no MDC.
O máximo divisor comum, representado pela sigla MDC, é o maior número que pode ser divisor de um ou mais números. O MDC pode ser obtido, por meio da decomposição em fatores primos.
Outros exemplo de MDC:
Exemplo 1. Obter o MDC entre 24 e 36.
Vamos decompor os números em fatores primos e comparar os resultados.

Comparando as decomposições, notamos que o produto 22 x 3 divide ambos os números. Repare que nas decomposições aparecem 2 fatores iguais a 2 e 1 fator igual a 3. Eles foram circulados para facilitar a compreensão. Logo, o MDC é 22 x 3 = 12.
Pode-se dizer também, que o MDC entre dois ou mais números pode ser obtido pelo produto dos fatores comuns, elevados às menores potências.
Exemplo 2. Calcular o MDC entre 45, 60 e 75.
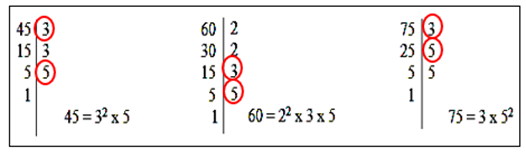
Nesse caso, os únicos fatores comuns foram 3 e 5. Eles aparecem destacados nos círculos. Logo, MDC (45, 60, 75) = 3 x 5 = 15
Vamos praticar o MDC! Resolva os exercícios abaixo em seu caderno.
01. Com base nas técnicas para se obter o MDC, calcule:
a) MDC entre os números 96 e 168;
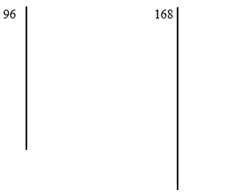
b) MDC entre os números 180 e 324.
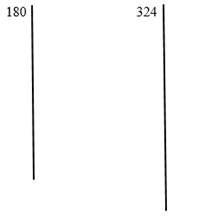
Um procedimento prático para encontrar o MMC e o MDC entre dois ou mais números consiste na decomposição simultânea (ao mesmo tempo). Veja este vídeo exemplificando.
Exemplo:
Calcular o MMC e o MDC entre 90 e 60. Faremos a decomposição em fatores primos dos dois números ao mesmo tempo. Caso não seja possível dividir algum número pelo mesmo divisor primo, ele será repetido nessa linha.
Observe os cálculos da decomposição simultânea.

2. Nos itens a seguir, calcule o MDC e o MMC entre os números dados.
a) MDC (35, 40) =
b) MMC (35, 40) =
c) MDC (20, 30, 25) =
d) MMC (20, 30, 25) =
e) MDC (12, 60) =
f) MMC (12, 60) =
3. Calcule o MMC entre os números abaixo:
a) 40 e 30 =
b) 20, 45 e 21=
c) 36, 28 e 34 =
d) 100 e 54 =
e) 24, 36 e 90 =
f) 100, 25, 50 =
4. Coloque V (verdadeiro) ou F (falso) nas sentenças.
( ) O MDC entre dois números é sempre o menor deles.
( ) O MMC entre dois números é sempre menor que o MDC entre eles.
( ) A decomposição simultânea de 24 e 50 é 22 x 3 x 5.
( ) O quociente de 300 pelo MDC (300,600) é 1.
( ) A metade do MMC (30,50) é 15.
( ) O MMC entre dois números é sempre o produto entre eles.
5. Responda.
a) Qual o menor número que dividido por 4 e 5 deixa o mesmo resto 2?
b) Qual o menor número que dividido por 2, 3 e 5 deixa o mesmo resto 1?
c) Qual o MDC entre 22 x 3 x 52 e 2 x 52 ?
d) Qual o MDC entre 3 x 53 x 7 e 32 x 52 x 11?
6. Problema dos enfeites
Regina possui 3 pedaços de fita, como os apresentados a seguir, que serão utilizados na confecção de alguns enfeites. Ela pretende cortá-los em pedaços do maior tamanho possível, de forma que não haja sobras e que todos os pedaços tenham o mesmo tamanho.
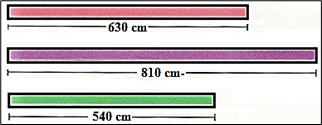
a) Qual será o tamanho de cada pedaço de fita após o corte?
b) Quantos pedaços de fita serão obtidos ao todo?
Lembrem-se de compartilhar essa atividade com seus colegas e com o seu professor.
Vamos parar por aqui. Até a próxima, pessoal!!!

Essa aula pra mim foi uma das mais interessante
Meus parabéns vcs sao feras na matemática