Aula 3 – Matemática 7° Ano - 22/04/2020
Oi galera!! Você conhece Roberto Carlos? Ele é um famoso cantor e compositor brasileiro. Leia o trecho de uma música do Roberto Carlos e Erasmo Carlos chamada “É preciso saber viver”:

Quem espera que a vida
Seja feita de ilusão
Pode até ficar maluco
Ou morrer na solidão
É preciso ter cuidado
Pra mais tarde não sofrer
É preciso saber viver
Toda pedra do caminho
Você pode retirar
Numa flor que tem espinho
Você pode se arranhar
Se o bem e o mal existem
Você pode escolher
É preciso saber viver
Você quer saber um pouco mais sobre esse cantor acesse o link abaixo e leia sua biografia.

https://www.ebiografia.com/roberto_carlos/
Vamos hoje aprender sobre sequências numéricas.
Sequências:
Ao estudar os conjuntos numéricos, você estudou algumas sequências numéricas, como a dos números naturais e a dos números inteiros.
Sequência dos números naturais: (0, 1, 2, 3, 4, 5, 6, …)
Sequência dos números inteiros: (…, – 4, – 3, – 2, – 1, 0, 1, 2, 3, …)
O nosso interesse aqui, é reconhecer as sequências que têm uma lei de formação, ou seja, uma regra que explica a relação entre os termos de uma sequência. Exemplo:
Números naturais pares: (0, 2, 4, 6, 8, …)
Veja o vídeo a seguir exemplificando.
Identificação de um termo da sequência
Quando queremos identificar a ordem (posição) em que um termo está disposto em uma sequência, podemos usar uma letra minúscula do nosso alfabeto, seguida de um índice subscrito.
(a1, a2, a3, a4, a5, …, an, …)
Por exemplo, considere a sequência formada pelos 6 primeiros múltiplos positivos de 3.
(3, 6, 9, 12, 15, 18, 21, …)
Nessa sequência, a1=3, a2 = 6, a3 = 9 e assim por diante.
Obs.: O índice (subscrito) indica a ordem (posição) do termo na sequência.
Sequência finita e sequência infinita
Uma sequência pode ser classificada como finita ou infinita.
Sequência finita: é aquela que tem um número finito de termos. Exemplo:
Números primos menores do que 10: (2, 3, 5, 7) Sequência infinita: Múltiplos naturais de 4: (4, 8, 12, 16, 20, …)
Vamos agora praticar! Resolva em seu caderno os seguinte exercícios.
01. Considere a sequência numérica (19, 16, 13, 10, 7, 4, x) cuja lei de formação é a1=19 e cada termo, a partir do segundo, é 3 unidades a menos que o anterior. Assim, temos x = 1. Observe agora as seguintes sequências, e determine o valor de x em cada uma delas.
a) (…, – 4, 0, 4, 8, 12, 16, 20, 24, x, …)
b) (5, 10, 20, 40, 80, x, …)
c) (1, 4, 9, 16, 25, 36, 49, x, …)
02. Considere a sequência (2, 5, 8, …, 14, …). Quais são os termos a4 e a6?
03. Considerando o que estudamos sobre sequências numéricas, qual número corresponde a letra m?

04. Determine os três próximos números da sequência (0, 5, 10, 15, 20, …).
05. Considere a sucessão de figuras apresentada a seguir, em que cada figura é formada por um conjunto de palitos de fósforo.
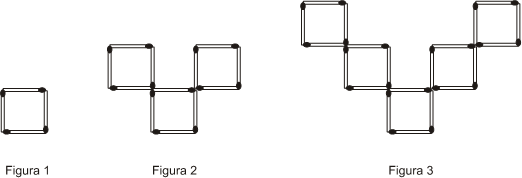
Quantos palitos são necessários para formar a Figura 5?
Lembrem-se de compartilhar essa atividade com seus colegas e com o seu professor.
Vamos parar por aqui. Até a próxima, pessoal!!!

Muito legal