Oi galera!! Você conhece Roberto Carlos? Ele é um famoso cantor e compositor brasileiro. Leia o trecho de uma música do Roberto Carlos e Erasmo Carlos chamada “É preciso saber viver”:

Quem espera que a vida
Seja feita de ilusão
Pode até ficar maluco
Ou morrer na solidão
É preciso ter cuidado
Pra mais tarde não sofrer
É preciso saber viver
Toda pedra do caminho
Você pode retirar
Numa flor que tem espinho
Você pode se arranhar
Se o bem e o mal existem
Você pode escolher
É preciso saber viver

Você quer saber um pouco mais sobre esse cantor acesse o link abaixo e leia sua biografia.

https://www.ebiografia.com/roberto_carlos/

Hoje vamos conhecer a dízima periódica e fração geratriz.

Números racionais – Dízima Periódica

O número 0,333… é chamado de decimal periódico não exato (dízima periódica), portanto podemos associar esse número a uma fração, denominada de fração geratriz. Logo, toda dízima periódica, deve possuir uma forma fracionária. Temos dois tipos de dízima periódica

Simples: o período começa a partir da virgula;

a) 0,2222…, período 2 (um algarismo)

b) 0,353535…, período 35 (dois algarismos)

c) 2,123123…, período 123 (três algarismos)

Composta: antes do período começar existem números denominados de antiperíodo que não fazem parte do período.

a) 0,3222…, período 2 e antiperíodo 3

b) 1,20333… período 3 e antiperíodo 20

c) 0,012515151… período 51 e antiperíodo 012

Para acharmos a fração geratriz de alguma dízima periódica seguimos alguns passos.

Veja no vídeo a seguir.

Relembrando

Para determinarmos uma fração geratriz vamos seguir os seguintes passos

1º passo: Igualar a dízima periódica a uma incógnita, por exemplo x, de forma a escrever uma equação do 1º grau.

2º passo: Dízima periódica simples – multiplicar ambos os lados da equação por um múltiplo de 10. Para descobrir qual será o múltiplo, devemos identificar quantos casas decimais devemos “andar” para que o período fique antes da vírgula. Dízima periódica composta multiplicar ambos os lados da equação por um múltiplo de 10, observando a quantidade de casas do antiperíodo. Depois repetir o mesmo processo da dízima periódica simples.

3º passo: Dízima periódica simples – diminuir a equação encontrada da equação inicial. Dízima periódica – diminuir a última equação encontrada da penúltima e isolar a incógnita.

Exemplo. Determine a fração geratriz do número 0,222…

1º passo: Igualar a dízima periódica a uma incógnita, por exemplo x, de forma a escrever uma equação do 1º grau.

x=0,222⋯

2º passo: Dízima periódica simples – multiplicar ambos os lados da equação por um múltiplo de 10. Para descobrir qual será o múltiplo, devemos identificar quantos casas decimais devemos “andar” para que o período fique antes da vírgula. Dízima periódica composta multiplicar ambos os lados da equação por um múltiplo de 10, observando a quantidade de casas do antiperíodo. Depois repetir o mesmo processo da dízima periódica simples.

x∙(10)=0,222⋯∙(10)⇒10x=2,22⋯

3º passo: Dízima periódica simples – diminuir a equação encontrada da equação inicial. Dízima periódica – diminuir a última equação encontrada da penúltima e isolar a incógnita.

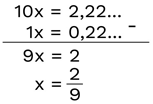
Será que podemos simplificar esse processo? Temos um método prático para encontrar a fração geratriz. Observe a imagem abaixo

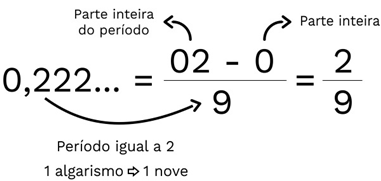
Exemplo 02. Determine a fração geratriz do número 0,3222…

1º passo: Igualar a dízima periódica a uma incógnita, por exemplo x, de forma a escrever uma equação do 1º grau.

x=0,3222⋯

2º passo: Dízima periódica simples – multiplicar ambos os lados da equação por um múltiplo de 10. Para descobrir qual será o múltiplo, devemos identificar quantos casas decimais devemos “andar” para que o período fique antes da vírgula. Dízima periódica composta multiplicar ambos os lados da equação por um múltiplo de 10, observando a quantidade de casas do antiperíodo. Depois repetir o mesmo processo da dízima periódica simples.

x∙(10)=0,3222⋯∙(10)⇒10x=3,22⋯ ⇒ 10x∙(10)=3,22⋯∙(10)⇒100x=32,22…

3º passo: Dízima periódica simples – diminuir a equação encontrada da equação inicial. Dízima periódica – diminuir a última equação encontrada da penúltima e isolar a incógnita.

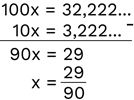
Vamos utilizar o método prático.

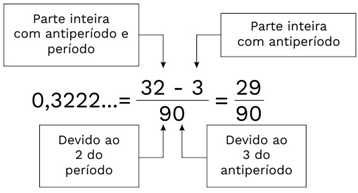
Exemplo 03. Determine a fração geratriz, usando o método prático, do número 1,02555…

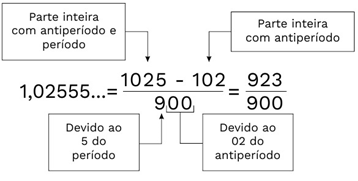
Agora vamos praticar! Resolva os seguintes exercícios em seu caderno.

01. Expresse na forma de fração os seguintes números racionais

a) 0,777….

b) 1,3232….

c) 1,444….

d) 0,033…

e) 2,35111…

02. (Enem 2015 – ADAPTADO) No contexto da matemática recreativa, utilizando diversos materiais didáticos para motivar seus alunos, uma professora organizou um jogo com um tipo de baralho modificado. No início do jogo, vira-se uma carta do baralho na mesa e cada jogador recebe em mãos nove cartas. Deseja-se formar pares de cartas, sendo a primeira carta a da mesa e a segunda, uma carta na mão do jogador, que tenha um valor equivalente àquele descrito na carta da mesa. O objetivo do jogo é verificar qual jogador consegue o maior número de pares. Iniciado o jogo, a carta virada na mesa e as cartas da mão de um jogador são como no esquema:

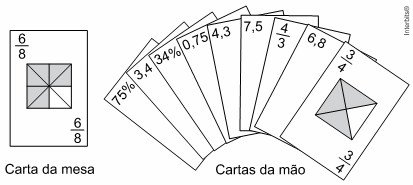
Segundo as regras do jogo, quantas cartas da mão desse jogador podem formar um par com a carta da mesa?

(A) 9   

(B) 7   

(C) 4   

(D) 3

03. O número real representado por 0,5222… é

(A) 52/9

(B) 47/9

(C) 47/90

(D) 47/99

04. (Ufrgs 2008) Se x = 0,949494… e y = 0,060606…, então x + y é igual a

(A) 1,11.

(B) 10/9.

(C) 100/99.

(D) 110/9.

05. (Pucrj 2007)  Escreva na forma de fração  a soma 0, 2222… + 0, 23333….

06. (Pucrj 2004)  A soma 1,3333… + 0,16666… é igual a:

a) 1/2

c) 4/3

c) 5/3

d) 3/2

Lembrem-se de compartilhar essa atividade com seus colegas e com o seu professor.

Vamos parar por aqui. Até a próxima, pessoal!!!