Fala galerinha! Vamos aprender hoje sobre congruência de triângulos.

Veja o vídeo abaixo e entenda melhor sobre.

Congruência

Quando comparamos duas figuras geralmente queremos saber quais as semelhanças existentes entre elas. Algumas vezes elas são iguais, algumas vezes são apenas parecidas e existem os casos em que as figuras comparadas são completamente diferentes. Na matemática, frequentemente as figuras geométricas são comparadas e os resultados possíveis são: Figuras congruentes, figuras semelhantes e figuras diferentes.

Vamos discutir a semelhança entre polígonos e os casos de semelhança entre triângulos.

Dois polígonos são semelhantes quando:

I. Existe proporcionalidade entre seus lados e;

II. Seus ângulos correspondentes são todos congruentes.

Existir uma razão de proporcionalidade quer dizer que se dividirmos a medida de um lado da primeira figura pelo valor de um lado da segunda figura e o resultado for, por exemplo, o número 3, então todas as divisões entre medidas de lados da primeira figura por medidas dos lados da segunda figura terão 3 como resultado.

Observe os retângulos ABCD e EFGH abaixo:

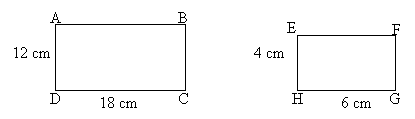
Perceba que eles são semelhantes, pois satisfazem as duas condições de semelhança.

I. Existe proporcionalidade entre os lados.

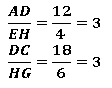
II. Seus ângulos correspondentes são todos congruentes.

Dois retângulos,portanto todos os ângulos internos são retos (90°)

Para os triângulos a regra é a mesma. Dois triângulos são semelhantes caso três ângulos correspondentes sejam congruentes e 3 lados correspondentes possuam a mesma razão de proporcionalidade.

Porém, é possível verificar a semelhança nos triângulos de uma forma mais simples. Basta observar se eles se enquadram em um dos casos de semelhança de triângulos a seguir:

Caso Ângulo Ângulo (AA): 

Dois triângulos são semelhantes se possuírem dois ângulos correspondentes congruentes.

Não é necessário verificar o terceiro ângulo e nenhuma proporcionalidade entre os lados. Basta que dois ângulos sejam congruentes e os dois triângulos já podem ser declarados semelhantes, como no exemplo a seguir:

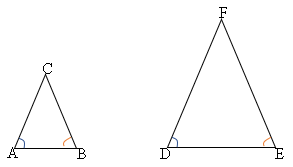
Perceba que o ângulo A é congruente ao ângulo D e o ângulo B é congruente ao ângulo E, ou seja,

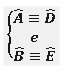
Caso Lado Lado Lado (LLL):

Se dois triângulos possuem três lados proporcionais, então esses dois triângulos são semelhantes. Portanto, não é necessário verificar os ângulos.

Observe os triângulos ABC e DFG abaixo:

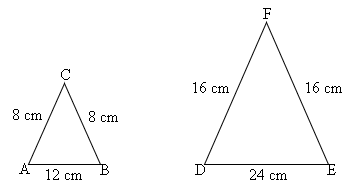
Na imagem acima, observe que as razões entre lados correspondentes têm o mesmo resultado:

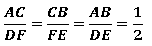
Então, pelo segundo caso de semelhança, esses triângulos são semelhantes.

Caso Lado Ângulo Lado (LAL):

Dois triângulos que possuem dois lados proporcionais e o ângulo entre eles congruente são semelhantes. 

Observe este caso de semelhança no exemplo:

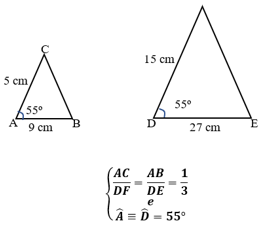
Nesse exemplo, o ângulo de 55 graus fica entre os lados proporcionais. Configurando assim o caso LAL.

Exemplo 1. Renata precisava medir a altura de uma árvore. Para isso, colocou um pedaço de cano enterrado no chão, formando um ângulo de 90º com o solo. Depois mediu os comprimentos das sombras da árvore do cano, obtendo as medidas indicadas na figura abaixo.

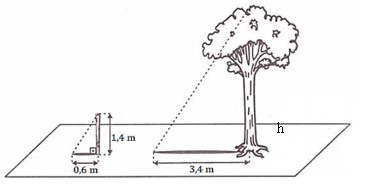
Qual é a medida aproximada da altura dessa árvore?

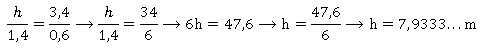
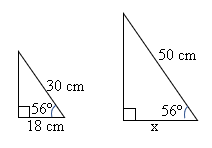
Exemplo 02. Qual o valor de x nos triângulos a seguir?

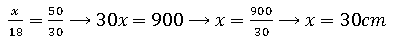
Vamos praticar! Resolva os exercícios em seu caderno.

01. Observe os triângulos da imagem a seguir e assinale a alternativa correta.

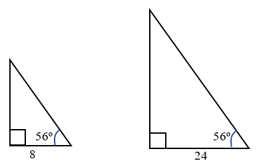
(A) Os triângulos são semelhantes, pois possuem o mesmo formato. Essa é a única maneira de descobrir se duas figuras geométricas são semelhantes.

(B) Os triângulos não são semelhantes, pois não existe caso de semelhança para quando se conhece apenas um lado e um ângulo de dois triângulos.

(C) Os triângulos são semelhantes pelo caso ALA (Ângulo – Lado – Ângulo).

(D) Os triângulos são semelhantes pelo caso AA (Ângulo – Ângulo).

02. A sombra de um prédio, num terreno plano, numa determinada hora do dia, mede 15 m. Nesse mesmo instante, próximo ao prédio, a sombra de um poste de altura 5 m mede 3 m.

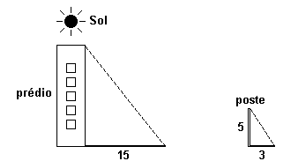
A altura do prédio, em metros, é:

(A) 25.

(B) 29.

(C) 30.

(D) 45.

(E) 75.

03. Às 10 h 45 min de uma manhã ensolarada, as sombras de um edifício e de um poste de 8 metros de altura foram medidas ao mesmo tempo. Foram encontrados 30 metros e 12 metros, respectivamente, conforme ilustração abaixo.

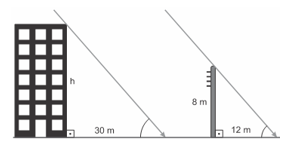
De acordo com as informações acima, a altura h do prédio é de:

(A) 12 metros.

(B) 14 metros.

(C) 18 metros.

(D) 20 metros.

04. O dono de um sítio pretende colocar uma haste de sustentação para melhor firmar dois postes de comprimentos iguais a 6m e 4m. A figura representa a situação real na qual os postes são descritos pelos segmentos AC e BD e a haste é representada pelo EF, todos perpendiculares ao solo, que é indicado pelo segmento de reta AB. Os segmentos AD e BC representam cabos de aço que serão instalados.

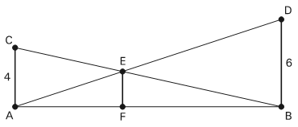
Qual deve ser o valor do comprimento da haste EF?

(a) 1 m

(b) 2 m

(c) 2,4 m

(d) 3 m

(e) 2√6 m

05. Qual o valor de x nos triângulos a seguir?

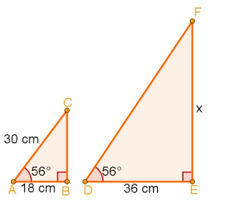
(A) 48 cm

(B) 49 cm

(C) 50 cm

(D) 54 cm

06. Na imagem a seguir, é possível perceber dois triângulos que compartilham parte de dois lados. Sabendo que os segmentos BA e DE são paralelos, qual a medida de x?

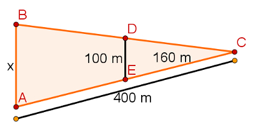
(A) 210 m

(B) 220 m

(C) 250 m

(D) 260 m

Ufa!! Acabamos por aqui!

Lembrem-se de compartilhar essa atividade com seus colegas e com o seu professor.

Até a próxima, pessoal!!!