Fala galera! Vamos aprender hoje sobre Bháskara e Equação do 2° Grau

NÚMERO DE OURO

O número de ouro, também conhecida como razão áurea, é identificada pela letra grega φ(lê-se Fi), em homenagem ao escultor Phideas (Fídias), que é a teria utilizado para conceber o Parthenon, e com o valor arredondado a três casas decimais de 1,618.

Para determinarmos algebricamente essa razão, vamos, primeiramente, tomar um segmento AB de medida 1 e um ponto C entre A e B dividindo o segmento AB na média e extrema razão. Ficou um pouco confuso? Observe o desenho e perceba que não é assim tão difícil.

Chamando de x a medida do segmento maior, AC, o valor da medida do segmento CB será 1 – x. De acordo com a definição de extrema razão, temos que:

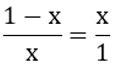
Aplicando a propriedade das proporções, chegamos a uma equação na incógnita x cuja solução, nesse caso, será conhecida como número de ouro.

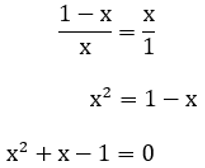
Portanto, o número de ouro será a solução de uma equação. Estudaremos o processo para o reconhecimento e resolução de equações como essa.

Equação do 2º grau

Um polinômio da forma P(x)=ax²+bx+c é dito polinômio do 2º grau de uma variável x, com a diferente de zero. Chamamos de equação do 2º grau ou equação quadrática na incógnita x a igualdade entre esse polinômio e o número zero.

Uma equação do 2º grau na forma P(x)=ax²+bx+c=0 é uma equação reduzida ou geral.

Veja o vídeo a seguir explicando melhor sobre o assunto.

Elementos da equação

Considere a equação do 2º grau ax²+bx+c=0, com a≠0.

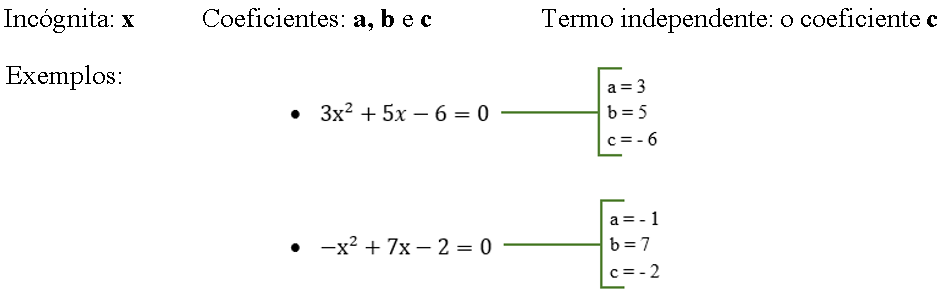
Equações completas e incompletas

Uma equação do 2º grau ax²+bx+c=0, com a≠0 é denominada:

Completa, quando b≠0 e c≠0, ou seja, todos os coeficientes da equação são diferentes de zero.

Exemplo:

9x²+3x+2=0 é uma equação completa, pois a=9,b=-3 e c=2.

Incompleta, quando b=0 e/ou c=2.

Exemplos:

x²+6x=0 é uma equação incompleta, pois a=1,b=6 e c=0.
-x²+4=0 é uma equação incompleta, pois a=-1,b=0 e c=4.
7x²=0 é uma equação incompleta, pois a=7,b=0 e c=0.

Raiz e/ou solução de uma equação

Os elementos do conjunto solução de uma equação são chamados raízes da equação. Para verificar se um número é raiz de uma equação, devemos fazer o seguinte processo:

1. Substituir a incógnita por esse número.

2. Determinar o valor de cada membro da equação.

3. Verificar a igualdade. Sendo uma sentença verdadeira, o número considerado é raiz da equação.

Na equação x²-6x+5=0, os valores 1 e 5 são raízes da equação. Vamos verificar essa afirmação utilizando os três passos descritos anteriormente.

Vamos verificar para o número 1.

01. Substituir a incógnita por esse número.
(1)²-6∙(1)+5=0

02. Determinar o valor de cada membro da equação.
(1)²-6∙(1)+5=0
1-6+5=0
-5+5=0
0=0 (verdadeira)

03. Verificar a igualdade. Sendo uma sentença verdadeira, o número considerado é raiz da equação.
Portanto o número 1 é raiz da equação.

Vamos verificar para o número 5.

01. Substituir a incógnita por esse número.

(5)²-6∙(5)+5=0

02. Determinar o valor de cada membro da equação.

(5)²-6∙(5)+5=0
25-30+5=0
-5+5=0
0=0 (verdadeira)

Verificar a igualdade. Sendo uma sentença verdadeira, o número considerado é raiz da equação.

Portanto o número 5 é raiz da equação.

Logo o conjunto solução é dado por S={1 ; 5}

Fórmula de Bhaskara

Essa fórmula é muito famosa e por mais que ela receba o nome desse matemático, ele não a desenvolveu e sim um conjunto de matemáticos brilhantes ao longo da História. Vamos conhecer essa fórmula, tão famosa?

O número b²-4ac é denominado discriminante e é simbolizado pela letra grega ∆ (lê-se delta). A Fórmula de Bhaskara pode também ser escrita como:

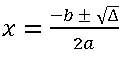
E as raízes da equação como:

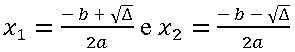
Com ∆ = b²-4ac. Fique tranquilo, a resolução desse tipo de equação é muito fácil.

Exemplo: Resolver a equação x²-6x+5=0 utilizando a Fórmula de Bhaskara.
1º passo: Identificar os coeficientes da equação

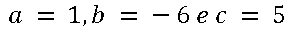
2º passo: Calcular o discriminante (∆)

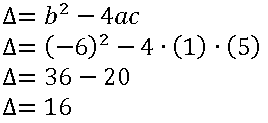
3º passo: Substituir na Fórmula de Bhaskara.

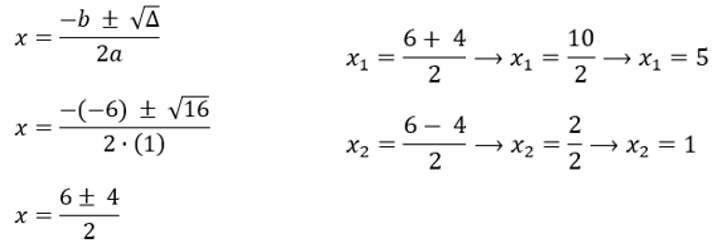
Exemplo: O nível de óleo em um reservatório varia com o tempo t, contado em horas, conforme a fórmula N = -t²+5t+6. Calcular o tempo, em horas, em que o nível do óleo desse reservatório chegará a zero.

Resolução: Perceba que o nível será zero, quando N = 0, ou seja, -t²+5t+6=0. Temos que resolver a equação dada. Utilizaremos a Fórmula de Bhaskara e seguiremos os passos do exemplo anterior.

1º passo: Identificar os coeficientes da equação

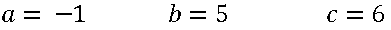
2º passo: Calcular o discriminante (∆)

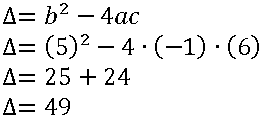
3º passo: Substituir na Fórmula de Bhaskara.

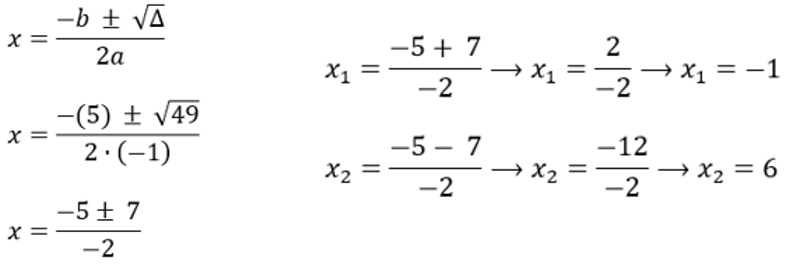
Como o tempo não pode ser negativo, temos que t = 6 horas.

No exemplo que acabamos de resolver, o nível N de óleo no reservatório depende do tempo t, ou seja, N depende de t. Nesta situação dizemos que a variável N está em função da variável t. Essa é uma função polinomial do 2º grau, ou simplesmente, função quadrática.

Exemplo. Sabendo que o número de ouro é a solução positiva da equação x²+x-1=0. O seu valor é igual a:

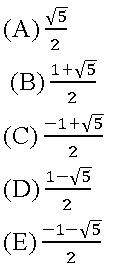
Agora pratique resolvendo os seguintes exercícios no caderno.

01. Identifique os coeficientes a, b e c, nessa ordem, de cada equação e associe as colunas I e II.

02. Observe a equação t²-5t+4=0. Marque a alternativa que indica suas soluções.

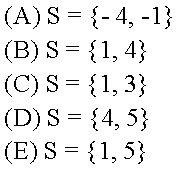
03. O nível de óleo em um reservatório varia com o tempo t, contado em horas, conforme a fórmula N = -t²+7t+18. Calcular o tempo, em horas, em que o nível do óleo desse reservatório chegará a zero.

04. As duas soluções de uma equação do 2° grau são – 3 e 1. Então a equação é:

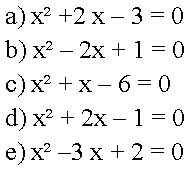
05. Resolva a equação do 2° grau 2x² + x – 3 = 0.

06. Determine a maior raiz da equação -2x² + 3x + 5 = 0.

07. A figura a seguir representa a vista superior de um apartamento no formato retangular. A área é 63 m2.

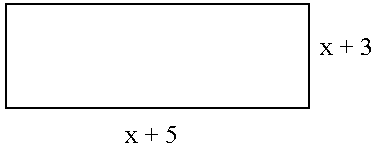
Observando a figura descrita acima, determine uma equação tendo por base a área da região retangular e em seguida calcule as dimensões do apartamento.

Ufa!! Acabamos por aqui!

Lembrem-se de compartilhar essa atividade com seus colegas e com o seu professor.

Até a próxima, pessoal!!!