Construções Geométricas – 7 ª Aula Matemática 8 ° Ano – 17/06/2020 - 18/06/2020
Olá pessoal! Vamos aprender sobre Construções Geométricas?
As construções geométricas utilizando régua e compasso seguem três princípios básicos. O primeiro deles é que, utilizando a régua, é sempre possível traçar uma reta, conhecendo-se dois pontos distintos. Além disso, com o compasso, é sempre possível traçar uma circunferência com centro em um ponto conhecido e que passa por um segundo ponto determinado. É também permitido obter pontos que podem ser construídos através de uma sequência de operações: intersecções de retas, intersecções de circunferências e intersecções de retas com circunferências.
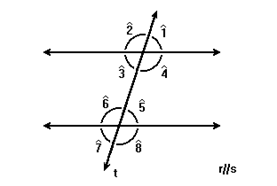
Acesso em: 31 de maio de 2020
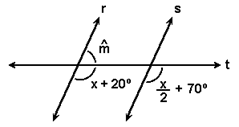
Acesso em: 31 de maio de 2020.
Com esses pontos obtidos, podemos traçar novas retas e novas circunferências e assim sucessivamente. A construção com estes instrumentos tem sido a marca registrada da Geometria, desde o aparecimento dos Elementos de Euclides, em torno de 300 a.C.
Construção da Mediatriz: Reta perpendicular que passa pelo ponto médio de um segmento, com régua e compasso.
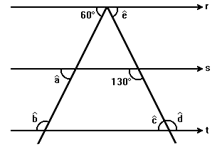
Construção da Bissetriz: Semirreta que divide o ângulo dado em dois ângulos congruentes, com régua e compasso.

Construção dos ângulos de 30°, 45° e 60° com régua e compasso.

Construção do ângulo de 90° com régua e compasso.

Construção do Pentágono Regular.



Construção do Hexágono Regular.


Algoritmo para a construção de um hexágono regular de qualquer área, a partir da medida do ângulo central.

Veja outros exemplos de polígonos.
Volume e sua unidade padronizada de medida:
É a grandeza indicada pela medida do espaço que um corpo ocupa, isto é, uma medida em três dimensões. A unidade padrão de volume é o metro cúbico, medida que indica o espaço ocupado por um corpo de dimensões 1 metro de comprimento, 1 metro de largura e 1 metro de altura. A partir do metro cúbico (m³), temos seus múltiplos – quilômetro cúbico (km³), hectômetro cúbico (hm³) e decâmetro cúbico (dam³) – e seus submúltiplos – decímetro cúbico (dm³), centímetro cúbico (cm³) e milímetro cúbico (mm³). Para a transformação das unidades de volume, usamos a tabela a seguir:

Exemplo 1.
Para transformar uma unidade de volume para outra, deslocando-se para a direita, deve-se multiplicar por 1 000 a cada unidade deslocada. Veja:
a) Transformar 2,45 km³ em hm³. De km³ para hm³, é uma casa para a direita, então:
2,45 km³ = 2,45 x 1000 = 2 450 hm³
b) Transformar 2 m³ em cm³. De m³ para cm³, são duas casas para a direita, então:
2 m³ = 2 x 1000 x 1000 = 2 000 000 cm³
Exemplo 2.
Para transformar uma unidade de volume para outra, deslocando-se para a esquerda, deve-se dividir por 1 000 a cada unidade deslocada.
Veja:
a) Transformar 53 000 mm³ em cm³. De mm³ para cm³, é uma casa para a esquerda, então:
5 3 000 mm³ = 53 000 : 1000 = 53 cm³
b) Transformar 194 700 dm³ para dam³. De dm³ para dam³, é uma casa para a esquerda, então:
194 000 dm³ = 194 000 : 1000 : 1000 = 0,194 dam³
Capacidade e sua unidade padronizada de medida
É a grandeza que estima a quantidade de líquido que ocupa um determinado recipiente. A unidade padrão de capacidade é o litro.
A partir do litro (L), temos seus múltiplos – quilolitro (kL), hectolitro (hL) e decalitro (daL) – e seus submúltiplos – decilitro (dL), centilitro (cL) e mililitro (mL).
Para a transformação das unidades de capacidade, usamos a tabela a seguir:

Exemplo.
Um carregamento de 20 caixas, cada uma contendo 6 garrafinhas de refrigerante com capacidade de 200 mL, chegou no Armazém das Capacidades. Qual é a medida desse carregamento, em litros?
Solução.
Multiplicando-se a quantidade de caixas pela quantidade de garrafinhas por caixa e pela capacidade de cada uma em mL, temos: 20 x 6 x 200 mL = 24 000 mL.
De mL para L, seguindo a tabela, são três casas para a esquerda. Dessa forma, podemos dividir por 10 a cada casa deslocada, ou ainda, deslocar com a vírgula três casas para a esquerda, ou apenas, cancelar três zeros, assim como fizemos para as medidas de comprimento.
Veja que dividir por 1000 (dividir por 10 e por 10 e por 10); deslocar a vírgula para a esquerda três casas ou simplesmente cancelar os três zeros, são maneiras equivalentes de se obter a mesma resposta: 24 000 mL = 24 L.
Relação entre as medidas de volume e as medidas de capacidade
Veja que a grandeza capacidade é específica para os estudos envolvendo o preenchimento de recipientes ou reservatórios no espaço, com líquidos. Volume é a grandeza que exprime a medida do espaço, que pode estar inicialmente vazio, ou ainda, preenchido com materiais sólidos, líquidos ou gasosos. No caso específico dos líquidos, como por exemplo a água, eles assumem a mesma forma que os recipientes que os contém, e por essa razão, podemos associar as medidas de capacidade com as de volume por meio das seguintes relações:

Volume de um Bloco Retangular: Um bloco retangular, nome popular do paralelepípedo reto retângulo, tem seu volume calculado pela seguinte fórmula: Volume = Área da Base x Altura
Se a base desse bloco é um retângulo de medidas a e b, e a altura desse bloco tem medida c, então podemos dizer que o volume desse bloco retangular será dado pelo produto de suas três dimensões, isto é:

Exemplo.
Calcular a capacidade, em litros, da piscina cujo formato é de um bloco retangular de medidas 8 m de comprimento, 5 m de largura e 1,60 m de profundidade.
Solução.
O volume dessa piscina (V) será dado pelo produto de suas dimensões, isto é:
V=8 x 5 x 1,6=64 m³.
Como para cada 1 m³ de volume tem-se 1 000 litros de capacidade, segue-se que a capacidade da piscina é de 64 000 litros.

As ilustrações apresentam corpos redondos em formato cilíndrico: lata de óleo, tanque de combustível, reservatório de gás, garrafa e copo são alguns dos exemplos encontrados no cotidiano. Para calcularmos a capacidade de um objeto com formato cilíndrico, precisamos encontrar a área da base circular e multiplicar pela altura do objeto. O cálculo da área do círculo é realizado multiplicando o quadrado da medida do raio pelo valor do número π (pi), cujo valor aproximado é igual a 3,14.
Para o cilindro reto, cujo raio da base é R, e cuja altura é H, calculamos o seu volume da seguinte forma:
Exemplo.
Calcular a capacidade, em mL, de uma lata de óleo cujo formato é um cilindro reto, cujo raio da base mede 3 cm e cuja altura mede 20 cm.
Solução.
Adotando-se π=3,14, o volume do cilindro reto de raio R = 3 cm e de altura H = 20 cm é dado por:
V=3,14 .(3)².(20) → V=3,14 .180 → V=565,2 cm³
Como para cada 1 cm³ de volume tem-se 1 mL de capacidade, segue-se que a capacidade da piscina é de 565,2 mL.
Hora de praticar! Resolva em seu caderno os seguintes exercícios.
1. Siga os passos da construção geométrica de um polígono a seguir.
Passo 1: Trace um segmento AB de medida 4 cm, utilizando uma régua.
Passo 2: Utilizando um compasso, com a ponta seca em A e abertura igual a 4 cm, trace um arco qualquer.
Passo 3: Com abertura do compasso 4 cm e ponta seca em B, faça um arco até formar uma interseção com o arco existente. Seja C esse ponto de interseção.
Passo 4: Ligue todos os pontos nomeados com segmentos de reta.
Nessas condições, responda:
a) Qual foi o polígono obtido?
b) Esse polígono é regular? Justifique sua resposta.
c) Calcule a soma dos lados desse polígono.
2. Observe os passos da construção geométrica a seguir.
Passo 1: Trace um segmento AB.
Passo 2: Fixe um ponto C do segmento AB.
Passo 3: Trace uma semicircunferência qualquer com centro em C.
Passo 4: Sejam D e E os pontos de interseção da semicircunferência com o segmento AB.
Passo 5: Trace a circunferência de centro em D, passando por E.
Passo 6: Trace a circunferência de centro em E, passando por D
Passo 7: Seja L um dos pontos de interseção das duas circunferências.
Passo 8: Considere a semirreta determinada por L e C.
Nessas condições, a medida do ângulo formado entre as semirretas (CL) ⃗ e (CB) ⃗ é igual a:
(A) 30°.
(B) 45°.
(C) 60°.
(D) 90°.
3. Construa usando instrumentos de desenho, um hexágono regular de lado igual a 6 cm.
4. Complete as lacunas a seguir:
a) A reta perpendicular que passa pelo ponto médio de um segmento é chamada de _________.
b) Os ângulos internos de um _______ medem 90°.
c) Os ângulos internos de um triângulo equilátero medem __________.
d) Uma semirreta cortou um ângulo de 240°, dividindo-o em dois ângulos com medidas iguais a 120°. Essa semirreta recebe o nome de _______.
e) O polígono que contém 5 lados com mesma medida recebe o nome de __________________.
5. Uma caixa em formato de bloco retangular foi dividida em cubos iguais que possuem 1 cm de aresta.
A capacidade máxima dessa caixa em litros, é igual a:
(A) 0,0006
(B) 0,006
(C) 0,06
(D) 0,6
6. Observe a imagem do copo com capacidade de 320 mL, a seguir. Qual é a diferença entre a capacidade do copo Long Drink e a capacidade de um copo com formato de cilindro reto, cujas medidas de diâmetro e altura são iguais as indicadas na imagem? Adote π=3,14.

(A) 210,66 mL
(B) 187,33 mL
(C) 111,16 mL
(D) 74,08 mL
7. Observe o bloco retangular na imagem ao lado.
O volume desse bloco tem medida igual a:

(A) 4 860 cm³.
(B) 2 430 cm³.
(C) 540 cm³.
(D) 111 cm³.
8. Uma indústria de embalagens deseja fabricar uma lata de tinta cilíndrica com raio da base medindo 5 cm de comprimento e com capacidade para 1 litro. Qual deverá ser o comprimento da altura dessa embalagem?
Adote π=3,14.
Ufa!! Acabamos por aqui!
Lembrem-se de compartilhar essa atividade com seus colegas e com o seu professor.
Até a próxima, pessoal!!!