Olá pessoal! Vamos aprender hoje sobre Equações do 2° grau com duas incógnitas.

Veja o vídeo a seguir que explica sobre.

Como esse estudo será voltado para sistemas de equações lineares, então, vamos entender primeiramente o conceito de uma equação linear.

Uma equação será dita linear quando puder ser escrita dessa forma:

a1 ·x1 + a2 ·x2 + a3 ·x3 +…+ an ·xn = k

Em que (a1,a2,a3,…,an) são os coeficientes da equação, (x1,x2,x3,…,xn) são as incógnitas e devem ser lineares e k é o termo independente.

As equações do 1º grau com duas incógnitas são representadas pela expressão ax + by = c, com a ≠ 0, b ≠ 0 e c assumindo qualquer valor real. Nesse modelo de equação, os valores de x e y estão ligados através de uma relação de dependência.

Veja as equações a seguir conforme sua quantidade de incógnitas.
-2x + 1 = -8 Equação linear com uma incógnita
5p + 2r =5 Equação linear com duas incógnitas
Para encontrarmos numa equação de 1º grau com duas incógnitas, por exemplo, 4x + 3y = 0, os valores de x e de y é preciso relacionar essa equação com outra ou outras com as mesmas incógnitas. Essa relação é chamada de sistema.

Exemplo

João usou apenas cédulas de R$ 20,00 e de R$ 5,00 para fazer um pagamento de R$ 140,00. Quantas cédulas de cada tipo ele usou, sabendo que no total foram 10 cédulas?

x cédulas de 20 reais y cédulas de 5 reais

Equação do número de cédulas: x + y = 10

Equação da quantidade e valor das cédulas: 20x + 5y = 140

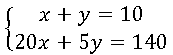
MÉTODO DA SUBSTITUIÇÃO

O primeiro passo consiste em escolher uma das equações e isolar uma das incógnitas. Assim,

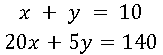
No segundo passo, basta substituir, na outra equação, a incógnita isolada no primeiro passo. Logo,

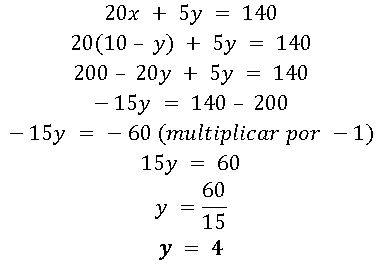
O terceiro passo, consiste em substituir o valor encontrado no segundo passo em qualquer uma das equações.

Assim,

x = 10 – 4→x = 6. Como x representa o número de cédulas de R$ 20,00 e y o número de cédulas de R$ 5,00, temos que João gastou 6 cédulas de 20 reais e 4 cédulas de 5 reais.

MÉTODO DA ADIÇÃO

Considere o mesmo sistema do exemplo 1.

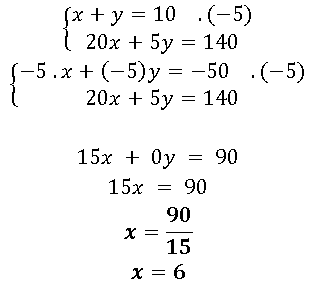
E substituindo o valor de x em qualquer uma das equações temos:

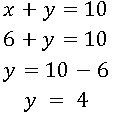
Portanto, a solução do sistema é S {(6, 4)}

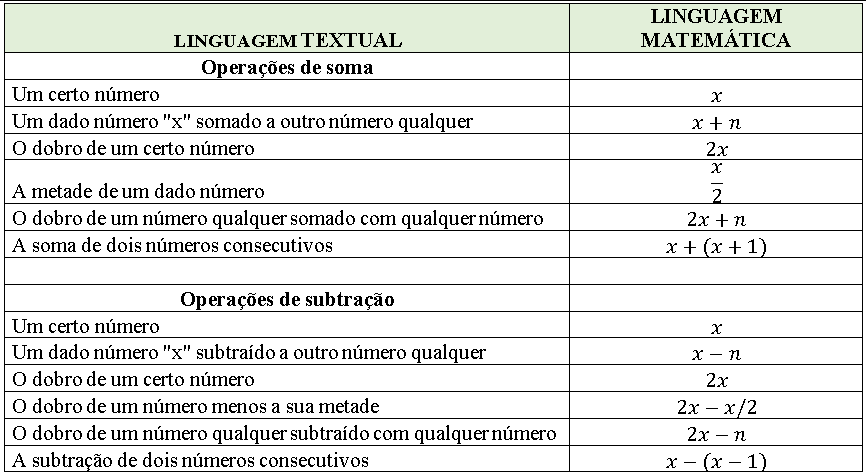
Equação polinomial de 2º grau do tipo ax² = b

EXEMPLO 1

Uma fazenda possuía 3 celeiros quadrados com o mesmo tamanho de lado para guardar arroz, feijão e trigo. A área total utilizada é de 300 m². Qual é a medida do lado do celeiro destinada para o armazenamento do arroz?

Vamos fazer um esboço da situação.

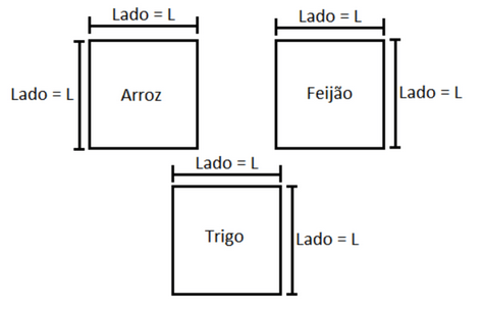
Observe que neste caso estamos considerando que a medida do lado é igual a um número L que ainda não sabemos qual é. Você pode considerar qualquer outra letra para representar esta medida.

Veja: se são quadrados de lado L metros, podemos dizer que cada um ocupa a área relativa a um quadrado de lado L, ou seja, L² metros quadrados.

Podemos dizer, então que temos:
L²+ L²+ L²=300

Ou seja,

3L²=300

Essa é a equação que podemos utilizar para traduzir o problema para a linguagem algébrica.

Agora, observe que:

3 x L²=3 x 100

Neste caso, concluímos que:

L²=100

Por isso, estamos procurando “de onde veio esse quadrado?”, ou seja, o número 100 é o quadrado de qual número?

L²=10²

Sabendo disso, chegamos a conclusão que L=10. Então o lado do celeiro em que o arroz é armazenado (assim como os outros celeiros) é igual a 10 metros.

Vamos praticar! Resolva em seu caderno os exercícios.

1. Observe o sistema de equações a seguir e encontre o valor de x e y e determine a solução do sistema.

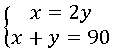
02. Xayane resolveu, em um final de semana, 36 exercícios de matemática a mais que Yara. Sabe-se que o total de exercícios resolvidos por elas foram 90.

Dessa forma é possível afirmar que o número de questões que Xayane resolveu é igual a:

(A) 63.

(B) 54.

(C) 36.

(D) 27.

3. A soma de dois números dados é 8 e a diferença entre estes mesmos números é igual a 4. Quais sãos os números?

4. A quantidade de pontos em um jogo de Alberto é o dobro da quantidade de pontos do Beto nesse mesmo jogo. Somando a pontuação dos dois tem-se o total de 150 pontos. Quantos pontos tem Alberto?

Dica: Indique a quantidade de pontos de cada um deles por uma incógnita (letra que representará um valor desconhecido)
Alberto = x e Beto = y

5. Em um abrigo para animais, entre gatos e cachorros, há 300 animais. Se o número de gatos é igual a metade do número de cachorros, determine quantas são o número de gatos e quantos são o número de cachorros.

6. Em um sítio existem cavalos, e galinhas, fazendo um total de 60 cabeças e 180 pés. Quantos são os animais de duas patas e quantos são os de quatro patas?

7. Para construir 3 paredes quadradas do seu banheiro, Arya precisou de 27 azulejos de 1 m² cada um. Qual é a medida da largura do banheiro de Arya?

(dica: utilize a equação 3x²=27 construída a partir dessa situação problema)

8. Determine o lado de um quadrado que é face de um cubo que possui superfície total medindo 150 cm².

9. Uma colcha com 10 retalhos quadrangulares idênticos possui uma superfície de 10m². Qual seria a medida do lado de cada retalho?

10. Um tapete possui uma área quadrada de 5m². Qual é a medida aproximada do lado deste tapete?

Ufa!! Acabamos por aqui!

Lembrem-se de compartilhar essa atividade com seus colegas e com o seu professor.

Até a próxima, pessoal!!!