Estudo de eventos probabilísticos -Atividade 4 - 05/03/2021
Estudo de eventos probabilísticos.
A parte da matemática que estuda o número de possibilidades de um evento ocorrer é denominada de Análise Combinatória. Em uma linguagem simplificada, a Análise Combinatória é a arte de contar. Nem sempre contar é um processo simples. Por exemplo:
No sorteio da Mega-Sena são sorteadas 6 dezenas escolhidas entre os números inteiros 1 e 60. De quantas formas distintas pode-se fazer essa escolha?
Logo de início podemos perceber que existe um número muito grande de possibilidades para montarmos um jogo em uma cartela e que é necessária certa técnica para determinarmos quantas possibilidades existem.
No entanto, tendo feito um determinado número x de jogos, um apostador passa a ter a chance de acertar os números que serão sorteados. Perceba que quanto maior for a quantidade de x, maior será a chance de acertar e receber o prêmio. O cálculo de quanto é essa “chance” é denominado de probabilidade.
Entendemos portanto que, para calcular a quantidade de possibilidades de ocorrência de um determinado acontecimento usamos os métodos de contagem da Análise Combinatória. Porém, quando queremos saber qual a chance de acontecer um resultado ou um conjunto de resultados específicos em meio a todas as possibilidades existentes, estaremos diante a Probabilidade de ocorrência desse ou desses resultados.
Probabilidade de um evento
Primeiramente temos que entender alguns conceitos preliminares.
➢ Espaço amostral ( U ): é o conjunto de todos os resultados possíveis do experimento.
Por exemplo: O lançamento de um dado com seis faces.
Neste caso, o conjunto de possibilidades de resultados é U = {1, 2, 3, 4, 5, 6}.
Perceba que para um conjunto com muitas possibilidades de resultados podemos lançar mão da Análise Combinatória para contar o número de elementos desse conjunto.
➢ Evento (E) é qualquer subconjunto do espaço amostral.
Por exemplo:
a) Evento 1 => faces números pares: {2, 4, 6};
b) Evento 2 => faces números múltiplos: {3, 6};
c) Evento 3 => faces números divisores de 60: {1, 2, 3, 4, 5, 6}.
d) Evento 4 => faces números múltiplos de 7: { }
Cálculo da Probabilidade
Seja um espaço amostral U e E um de seus eventos, denomina-se probabilidade do evento E o número P(E) obtido fazendo-se o quociente entre o número de elementos do evento E e o número de elementos do espaço amostra (U).
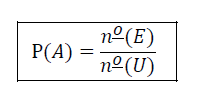
No exemplo anterior:

Podemos perceber que se o evento tem todos os elementos do espaço amostral sua probabilidade é 1 ou 100% e é chamado de evento certo. Se o evento é uma subconjunto vazio do espaço amostral sua probabilidade é zero “0” e é chamado de evento impossível, assim:
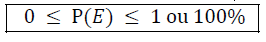
Adição de Probabilidades (UNIÃO)
Se A e B são dois eventos de mesmo espaço amostral.
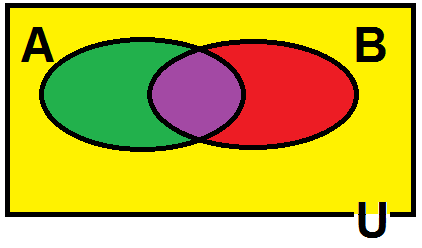
Podemos escrever que o número de elementos de AUB é dado pela expressão:
A∪B = A + B – A∩𝐵
dividindo por U, temos:
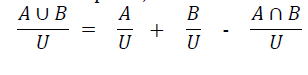
por definição:
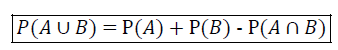
Observação:
✓ Se A ∩ B = ∅ ⇒ P(AUB) = P(A) + P(B), os eventos A e B são dijuntos.
Exemplo 02. Em uma pesquisa realizada sobre a preferência entre determinadas redes sociais, foram consultadas 470 alunos de uma escola estadual e o resultado foi que 250 preferem a rede “F”, 170 preferem a rede “I” e 50 gostam das duas. Escolhendo ao acaso um dos entrevistados, qual a probabilidade deste ter:
a) preferência pelas redes F e I, simultaneamente?
b) preferência pelas revistas F ou I?

Probabilidade de Eventos Complementares
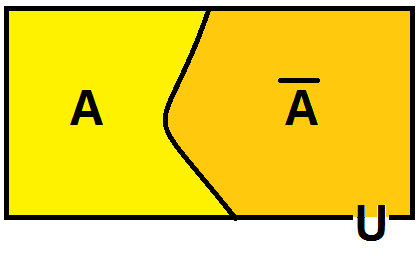
Sejam A e A̅ dois eventos complementares, então:
A ∪ 𝐀̅ = U, ou seja, quando unidos o resultado é o universo;
A ∩ 𝐀̅ = Ø, não possuem elementos em comum.
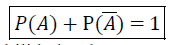
Observação: “O somatório de todas as probabilidades de um experimento é sempre igual a 1 ou 100%”.
Exemplo 03. Em uma sala de aula existem 17 alunos dos quais 7 são homens. Seu uma pessoa desta sala for
sorteada para uma determinada apresentação de um trabalho, qual a probabilidade dela:
a) ser uma mulher;
b) não ser uma mulher.
Solução:
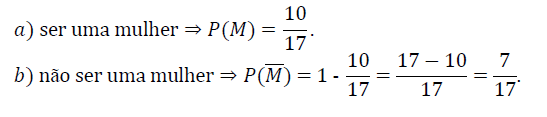
- Multiplicação de Probabilidades
Se um acontecimento é composto por vários eventos SUCESSIVOS e INDEPENDENTES, de tal modo
que:
o 1º evento é A e sua probabilidade e P(A);
o 2º evento é B e sua probabilidade é P(B);
o 3º evento é C e sua probabilidade é P(C);
. . . . .
o K-ésimo evento é K e sua probabilidade é P(K),
então, a probabilidade de que os eventos A, B, C, … , K do acontecimento ocorram NESSA ORDEM é:
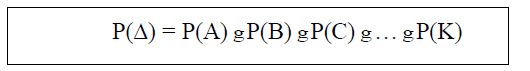
Exemplo 04. Em um baralho de 52 cartas, quatro cartas são retiradas aleatoriamente, sucessivamente e sem
reposição. Deixando os cálculos indicados, determine a probabilidade de as cartas retiradas serem:
a) 4 damas;
b) um ás, um valete, uma dama e um rei, nessa ordem;
c) três cartas de paus e uma de ouros, nesta ordem.♣♠
Resolução:
𝑎) 4 damas

ATIVIDADES
01) A probabilidade de um dos cem números 1, 2, 3, 4, …, 100 ser múltiplo de 6 e de 10 ao mesmo tempo é:
a) ( ) 3%.
b) ( ) 6%.
c) ( ) 2%.
d) ( ) 10%.
P() = P(A) gP(B) gP(C) g… gP(K)
02) Em uma pesquisa realizada sobre a preferência de duas revistas, foram consultadas 400 pessoas e o resultado foi que 200 leem a revista A, 150 leem B e 60 leem as duas revistas.
Escolhendo ao acaso um dos entrevistados, qual a probabilidade de ter:
a) preferência pelas revistas A e B?
b) preferência pelas revistas A ou B?
03) Em um determinado setor de um hospital, a probabilidade de um indivíduo estar com Covid 19 é estimada em 70/1000, a probabilidade dele estar com Pneumonia é 40/1000 e a probabilidade de um indivíduo estar com a duas doenças é de 15/1000.
Nesse caso, “estar com Pneumonia” não exclui a possibilidade de “estar com a COVID 19”.
Com base nessas informações, a probabilidade de um indivíduo, escolhido ao acaso, ser mudo ou cego é igual a:
a) ( ) 0,095.
b) ( ) 0,070.
c) ( ) 0,040.
d) ( ) 0,015.
04) Uma fábrica produz sucos com os seguintes sabores: uva, pêssego e laranja. Considere uma caixa com 12 garrafas desses sucos, sendo 4 garrafas de cada sabor.
Retirando-se, ao acaso, 2 garrafas dessa caixa, uma após a outra. Nestas condições, a probabilidade de que ambas garrafas sejam de uva é:
a) ( ) 1/3.
b) ( ) 1/12.
c) ( ) 1/11.
d) ( ) 1/4.
05) Uma caixa contém 15 bolas, sendo que 4 são azuis, 5 são vermelhas e 6 são brancas. Três bolas serão retiradas dessa caixa, uma após a outra e sem reposição. Nestas condições.
Determine a probabilidade de as bolas retiradas serem:
a) todas azuis;
b) todas vermelhas;
c) todas brancas:
06) Um jovem, querendo telefonar para sua namorada, percebe que esqueceu o último dígito do número da moça, e então decide tentar acertar o dígito que falta na sorte.
Qual a probabilidade de o jovem acertar o último dígito que falta só na terceira tentativa?
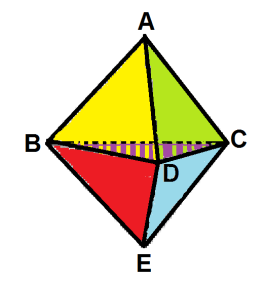
07) Dado um poliedro com 5 vértices e 6 faces triangulares, escolhem-se ao acaso três de seus vértices.
A probabilidade de que os três vértices escolhidos pertençam à mesma face do poliedro é:
a) ( ) 3/10.
b) ( ) 1/6.
c) ( ) 3/5.
d) ( ) 1/5.
08) Em uma central de atendimento, cem pessoas receberam senhas numeradas de 1 até 100. Uma das senhas é sorteada ao acaso.
Qual é a probabilidade de a senha sorteada ser um número de 1 a 20?
a) ( ) 1/100
b) ( ) 19/100
c) ( ) 20/100
d) ( ) 21/100
09) Numa classe com 60 alunos, 40 estudam Matemática, 25 estudam Ciências e 10 estudam Matemática e Ciências.
Se um aluno for sorteado ao acaso, determine a probabilidade desse um aluno:
a) estudar Matemática;
b) estudar Ciências;
c) estudar Matemática e Ciências;
d) estudar Matemática ou Ciências;
e) não estudar nem Matemática e nem Ciências.
10) Em uma escola existem 80 alunos do 1º ano, 70 alunos do 2º ano e 50 alunos do 3º ano. Serão sorteados 3 alunos para um congresso estudantil em Brasília. Nestas condições, qual a probabilidade de sortear um aluno de cada série?
“A persistência é o caminho do êxito.”
Charles Chaplin
]
“A persistência é o caminho do êxito.”
Charles Chaplin
NÃO ESQUEÇA DE IMPRIMIR SUA ATIVIDADE!!!
