Olá galerinha! Vamos aprender hoje sobre Fração.

O CONCEITO DE FRAÇÃO:

Em diversas ocasiões da vida cotidiana, nos deparamos com a necessidade de efetuar divisões e repartições, sobretudo, diante de uma pizza tamanho família:

Nesse exemplo, a melhor maneira é a repartição equitativa, isto é, dividir o inteiro em partes iguais. Cada uma dessas partes é chamada de fração de um inteiro, ou simplesmente, fração.
Assim, em uma pizza dividida em 8 pedaços iguais, cada parte representa uma fração de 1/8 da pizza inteira. Tendo 16 desses pedaços, podemos obter o equivalente a duas pizzas inteiras, uma vez que 16/8 corresponde à divisão dos dois números, isto é, 16 : 8 que resulta em 2.
E isso nos faz refletir nas operações envolvendo frações, pois elas traduzem equivalências, proporções e outras ideias matemáticas presentes na culinária, na construção civil, no sistema monetário, dentre outros.

Veja antes este vídeo explicando sobre:

Vejamos agora alguns conceitos sobre FRAÇÕES:

NÚMEROS RACIONAIS: O conjunto dos números racionais é dado pela coleção de todos os números que podem ser escritos sob a forma de fração, ou seja, são resultados de uma divisão entre dois números naturais, ditos numerador e denominador da fração.

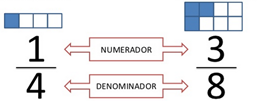
FRAÇÕES APARENTES: Se a divisão dos dois números apresentados na fração resulta em um número natural, dizemos que a fração é aparente.

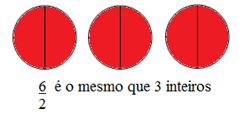
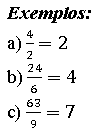
Note que em todos esses casos, o numerador é múltiplo do denominador.

FRAÇÕES PRÓPRIAS: Se a divisão dos dois números apresentados na fração resulta em um número entre 0 e 1, dizemos que a fração é própria.

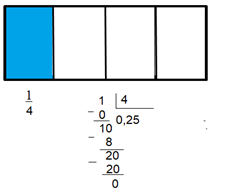
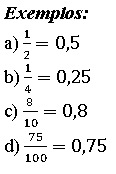
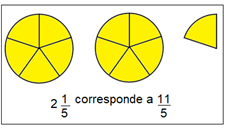
FRAÇÕES IMPRÓPRIAS E NÚMEROS MISTOS: Se a divisão dos dois números apresentados na fração resulta em um número maior que 1 e não natural, dizemos que a fração é imprópria.

Toda fração imprópria pode ser escrita como a soma de um número natural (fração aparente) com uma fração própria.

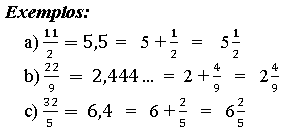
Vamos verificar os números mistos que são obtidos a partir das frações 41/7, 491/13 e 91/11, a seguir:

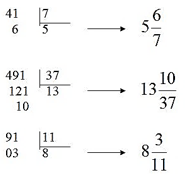
Assim, temos que:

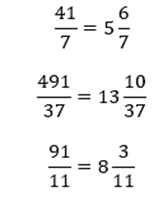
Logo, temos que no número misto:

O número natural é o quociente da divisão usando o método da chave.A fração própria é dada pela divisão entre o resto e o divisor.

Para transformar números mistos em frações impróprias, basta multiplicar o denominador pelo número natural e somar esse resultado ao numerador.

Veja:

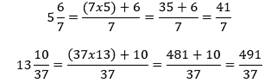
Percebemos que os números racionais, obtidos a partir de frações próprias ou impróprias, apresentam uma notação especial separando o número natural maior do que ou igual a zero antes da vírgula dos outros algarismos após a vírgula.

O número natural, à esquerda da virgula deverá ser lido com o acréscimo da palavra “inteiro” ou ainda “inteiros”.

A cada ordem após a vírgula lemos décimos, centésimos, milésimos, décimos de milésimos e assim por diante.

Se a quantidade de algarismos após a vírgula for finita, lemos o número (composto por todos os algarismos após a vírgula) acrescido da palavra que representa a última ordem decimal para a direita.

  Veja:

Veja:

0,1 à um décimo.

0,12 à doze centésimos.

0,125 à cento e vinte e cinco milésimos.

Podemos usar a palavra razão para substituir a palavra fração. No entanto, o conceito de razão, leva em conta um aprofundamento nos conhecimentos de frações. Vamos estudar dois conceitos especiais: as frações irredutíveis e as frações equivalentes.

FRAÇÕES EQUIVALENTES: Representam a mesma quantidade, possuem a mesma representação decimal, ou seja, são frações cujos resultados das divisões indicadas são iguais. Esse resultado em comum pode ser chamado de constante de proporcionalidade. Cada fração equivalente em uma proporção, pode ser chamada individualmente de razão.

Exemplo:

As frações 3/4 e 12/16 resultam ambas no decimal 0,75.

Podemos assim, escrever:

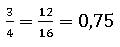
E interpretar que  e  são frações equivalentes.

Podemos ainda dizer que ambas são razões, cuja constante de proporcionalidade é 0,75.

Em particular,  é uma fração que não se podem dividir, numerador e denominador, por um mesmo número natural.

Veja que 12/16 é uma fração em que se pode dividir tanto numerador, quanto o denominador por 4.

Logo, percebemos que a fração 12/16, ao ser simplificada dividindo-se por 4, tanto numerador, quanto denominador, resulta em 3/4, que por sua vez não se pode simplificar.

Note que, encontrar a constante de proporcionalidade pela divisão 3/4, é bem mais simples do que na divisão 12/16, ou ainda, de outra fração equivalente a estas duas, como 192/256.

FRAÇÕES IRREDUTÍVEIS: São as frações que não se podem simplificar. São também as representações fracionárias mais simples das constantes de proporcionalidade em frações equivalentes.

Vamos agora praticar! Resolva em seu caderno os seguintes exercícios.

1. Faça a representação gráfica de cada uma das frações a seguir, conforme o exemplo:

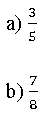
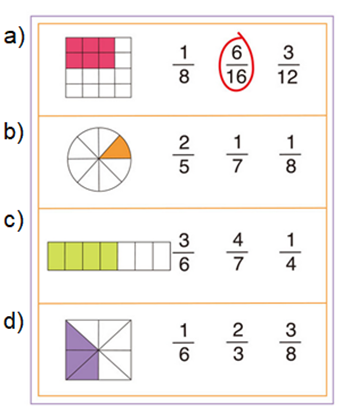
2. Indique a fração correspondente à parte colorida em cada figura, como mostra o exemplo a seguir.

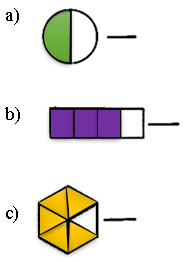
3. Determine a fração que representa a parte colorida em cada um dos seguintes casos:

4.  Um vendedor tinha 25 carros no pátio da concessionária. No mês de maio, em uma promoção, ele vendeu 16 carros.

Considerando-se o total de carros, qual é a fração que representa o número de vendas de carros efetuadas por esse vendedor no mês de maio?

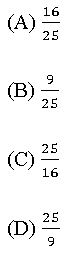
5.  Sabendo que as frações a seguir são todas aparentes, descubra o valor desconhecido # em cada caso:

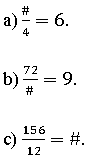
6.  Observe o número a seguir.

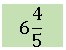
A fração imprópria que se obtém a partir desse número é igual a:

7.  Transforme as frações a seguir em números decimais e depois escreva como se lê esses números.

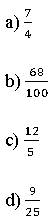
8.  Na reta numérica a seguir, cada marcação para a direita de zero corresponde a 0,1, ou seja, um décimo.

P está na quinta marcação após 7 inteiros e Q está na segunda marcação após 9 inteiros.

Os números representados pelos pontos P e Q são:

9.  Na turma da professora Ângela estão matriculados 24 meninos e 16 meninas. Determine:

a) A razão (fração irredutível) entre o número de meninos e o número de meninas.

b) A razão (fração irredutível) entre o número de meninas e o total de estudantes.

10. Vinícius parou em um posto de gasolina e colocou 20 litros de gasolina, completando o tanque, cuja capacidade máxima é de 60 litros.

A razão da gasolina que havia no tanque desse carro, em relação à sua capacidade máxima, é equivalente a:

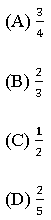
Ufa!! Acabamos por aqui!

Lembrem-se de compartilhar essa atividade com seus colegas e professores.

Até a próxima, pessoal!!!