Fala galera! Vamos aprender hoje sobre Frações Equivalentes e Irredutíveis.

Ao multiplicarmos ou dividirmos o numerador e o denominador de uma fração pelo mesmo número natural, diferente de zero, o resultado será uma outra representação da mesma fração. Frações obtidas assim, são ditas equivalentes. Definimos também que, se uma fração não admite divisão do numerador e do denominador simultaneamente por um mesmo número natural, então, essa fração é irredutível.

Veja o vídeo a seguir explicando melhor sobre o assunto.

Lembrando que frações são escritas de duas maneiras, com o numerador acima de denominador e a outra forma forma é do numerador ser separado do denominador por ” / ” de forma linear. Como:

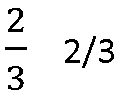
Sendo a mesma fração escrita de forma diferente.

Veja o exemplo de multiplicação de frações a seguir a seguir:

Ao multiplicarmos o numerador e o denominador da fração 2/3 por 2, obtemos a fração 4/6 e ambas representam a mesma fração.

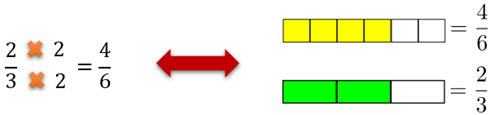
Dizemos que a fração 4/6 é equivalente à fração 2/3, pois representam a mesma quantidade. Além disso, observamos que na fração 2/3, o numerador e o denominador não podem ser divididos simultaneamente por um mesmo número natural. Dizemos então, que a fração 2/3 é irredutível.

Fração de uma quantidade.

Para calcular o valor correspondente à fração de uma quantidade, basta dividir a quantidade pelo denominador e multiplicar o resultado pelo numerador da fração.

Exemplo. Mariana recebe um salário de R$ 4 950,00 e decide poupar um terço dessa renda para investir na compra de um imóvel. Qual é o valor que Mariana destina para essa poupança?

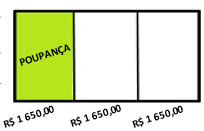
Solução. Para saber o valor que corresponde a 1/3 de R$ 4 950,00, basta dividir 4 950,00 por 3, cujo resultado é 1 650,00 e multiplicar o resultado por 1. Dessa forma, Mariana destina exatamente R$ 1 650,00 para essa poupança.

Adição e Subtração de frações com denominadores iguais.

Conservamos o denominador e fazemos a operação indicada entre os numeradores.

Exemplo. Para efetuar a operação 4/7+2/7 devemos conservar o denominador 7 e proceder com a soma indicada entre os numeradores. Veja:

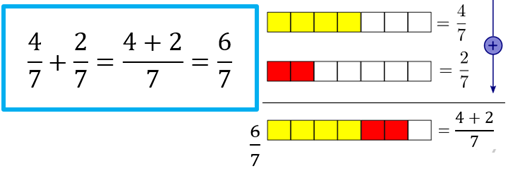
Adição e Subtração de frações com denominadores diferentes

Devemos obter frações equivalentes com mesmo denominador para efetuarmos adição e subtração de frações com denominadores diferentes. Para agilizar a obtenção das frações equivalentes, basta calcular o mínimo múltiplo comum (mmc) entre os denominadores das frações dadas.

Exemplo. Vamos efetuar a operação 3/7+2/5.

Solução. Primeiro calculamos o mmc (7 ; 5). Como 5 e 7 são números primos, então:

mmc (5 ; 7)= 5 x 7= 35.

Depois, obtemos as frações equivalentes com denominador 35 para as frações dadas:

Finalmente, como os denominadores estão iguais, podemos efetuar a operação indicada entre os numeradores. Veja:

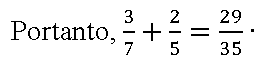
Transformações de frações em decimais

Em algumas situações, transformar frações em decimais pode facilitar as operações, sobretudo quando os denominadores são 2, 4, 5 ou 10. Para isso, basta utilizar as relações:

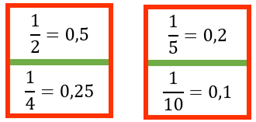
Exemplo. Vamos efetuar a operação 1/2 + 1/10 – 1/5∙

Solução. Substituindo as frações dadas por suas representações decimais equivalentes, obtemos 0,5 + 0,1 – 0,2 = 0,4.

Como 0,4 = 4/10=2/5, então:

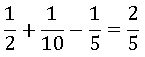
Agora pratique resolvendo os seguintes exercícios no caderno.

01. Leia o texto a seguir sobre a simplificação de frações:

Para simplificar frações, basta dividir numerador e denominador pela mesma quantidade, até que não seja mais possível simplificar. Mas, isso pode demorar muito se os números forem grandes e o processo usar apenas números primos como 2, 3 ou 5. A ideia aqui é que você simplifique de uma só vez, dividindo pelo maior número possível: o máximo divisor comum. Por exemplo, para simplificar a fração 36/63 basta dividir o numerador e o denominador pelo mdc (36, 63), que é igual a 9.

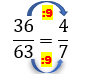
Com base na leitura, simplifique as frações a seguir, até obter uma fração irredutível.

02. Um tanque de um combustível, com capacidade de 24 litros, inicialmente vazio, é abastecido. Determine a quantidade de litros utilizados, se a fração solicitada pelo motorista foi:

03. Izabela e Leandro estão comendo uma pizza. Se Izabela já comeu 1/8 e Leandro comeu 3/8 dessa mesma pizza, responda:

a) Qual é a fração que representa a parte da pizza que foi comida?

b) Qual é a fração da pizza que sobrou?

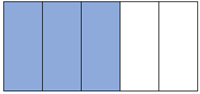
04. Leonardo e Mário herdaram um terreno de maneira que 3/5 do terreno ficou com Mário (parte azul da figura) e os 180 metros quadrados restantes ficaram com Leonardo. Nessas condições, a medida da área total do terreno, em metros quadrados, é igual a:

5. Resolva as operações de adição e subtração de frações a seguir.

Dica: Lembre-se de encontrar frações equivalentes usando o mmc.  

6. Dóris tem R$ 210,00 e vai ao shopping. Ela gastará 2/3 do dinheiro com roupas, 1/7 para assistir a um filme no cinema e guardará o restante.

a) Quanto Dóris gastará com roupas?

b) Quanto Dóris gastará com o cinema?

c) Quanto Dóris guardará após estes gastos?

d) Que fração do dinheiro será gasta por Dóris?

e) Que fração do dinheiro de Dóris sobrará?

7. Qual  das  alternativas  abaixo  apresenta uma expressão numérica cujo resultado é mais próximo de 2?

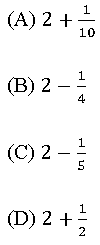
8. Observe a reta numerada a seguir. 

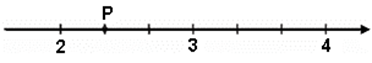
Sabe-se que cada unidade de medida foi dividida em partes iguais.

Qual é a fração que representa o ponto P?

Ufa!! Acabamos por aqui!

Lembrem-se de compartilhar essa atividade com seus colegas e com o seu professor.

Até a próxima, pessoal!!!