Função Quadrática – 5 ª Aula Matemática 9 ° Ano – 03/06/2020 - 03/06/2020
Olá pessoal! Vamos aprender hoje sobre Função Quadrática.
Função Quadrática:
Uma aplicação f de “R” em “R” recebe o nome de função quadrática ou do 2º grau quando associa a cada x ∈”R” o elemento (ax2 + bx + c) ∈R, em que a, b e c são números reais dados e a diferente de 0.
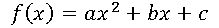
Veja o vídeo a seguir para entender melhor.
Exemplos de funções quadráticas:
f(x)=2x²+3x-1
f(x)=x²-2x-5
f(x)=-3x²+5x
f(x)=x²-4
f(x)=2x²
f(x)=x²
Gráfico:
O gráfico da função quadrática é uma parábola. Vamos construir o gráfico da função f(x)=x².
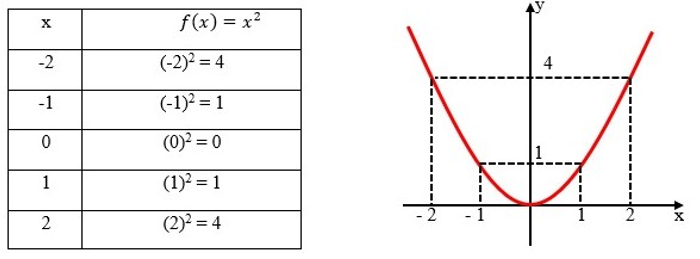
Agora vamos construir o gráfico da função f(x)=-2x²
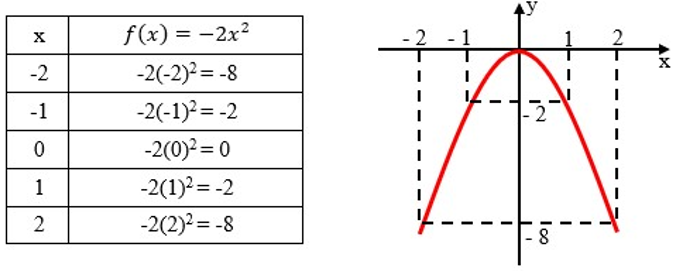
Perceba que o gráfico da função f(x)=x² possui a concavidade voltada para cima e o gráfico da função f(x)=-2x² possui a concavidade voltada para baixo. Quem determina essa concavidade é o valor do coeficiente que multiplica x². Se esse número for positivo, concavidade voltada para cima e se for negativo, concavidade voltada para baixo.

Coordenadas do vértice:
O vértice da parábola é o ponto onde a parábola troca o seu ramo, e vamos representá-lo por (V). Os pontos mínimo e de máximo são calculados pelas coordenadas do vértice.
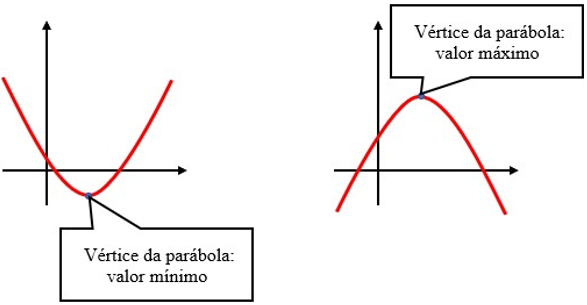
Para determinarmos os valores de x e y do vértice utilizaremos as seguintes fórmulas,

Portanto o vértice é dado pelas coordenadas,
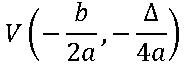
Exemplo 01. Determine as coordenadas do vértice da parábola definida pela função y=x^2-2x-5.
Resolução:
1º passo: Identificar os coeficientes
a = 1
b = – 2
c = – 5
2º passo: Calcular o x do vértice.
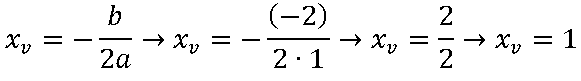
3º passo: Calcular o y do vértice.
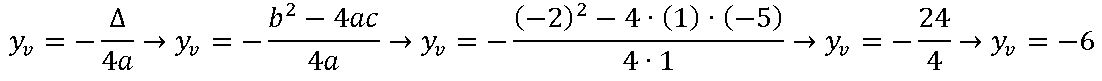
4º passo: Escrever as coordenadas do vértice.
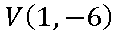
Exemplo 02. A dona de uma loja observou que o lucro (L) de sua loja dependia da quantidade de clientes (c) que frequentava o mesmo diariamente. Um matemático analisando a situação estabeleceu a seguinte função:
L(c) = – c² + 60c – 500
Qual seria o número de clientes necessário para que a dona da loja obtivesse o lucro máximo em seu estabelecimento?
(A) 28
(B) 29
(C) 30
(D) 32
(E) 34
Resolução: Perceba que o exercício pede para determinar a quantidade de clientes para que o lucro seja máximo. Note ainda que o c está representando o x e L(c) está representando o y. Basta calcularmos o x do vértice.
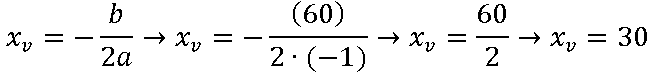
Logo, o número de clientes necessário para que a dona da loja obtenha o lucro máximo em seu estabelecimento é igual a 30.
Pratique agora em seu caderno com os próximos exercícios.
01. A respeito da função f(x) = – 4x2 + 100, determine o resultado da soma entre as coordenadas x e y do vértice.
02. A equação da trajetória parabólica do salto de uma pulga é dada por f(x) = –x2 + 4x. Essa pulga salta no ponto de origem do sistema de coordenadas cartesianas. Qual é, em decímetros, a altura máxima atingida pela pulga?
03 – Dada a função T(h) = –h2 + 22h – 85, em que h representa as horas do dia e T a temperatura. Calcule a temperatura máxima.
04 – Em uma empresa, o número de unidades diárias vendidas, x dias após o lançamento de um produto, pode ser modelado pela fórmula y = –x2 + 60x + 100, em que x = 0 é o dia do lançamento. Após atingir o maior número de unidades vendidas desse produto em um único dia, a fórmula deixa de ser válida e o número de produtos vendidos a cada dia começa a diminuir até que o produto deixa de ser vendido. Determine o número de dias, incluindo o dia do lançamento, até que o produto atinja o maior número de unidades diárias vendidas.
05 – Uma indústria produz x unidades por dia de um determinado produto que é vendido em sua totalidade a um preço de R$ 80,00 a unidade. O custo total para a produção diária de x unidades é igual a C (x) = x2 + 20x + 500.
Para que a indústria tenha um lucro diário L máximo, qual deve ser o número de unidades produzidas e vendidas por dia?
06 – Uma bola é lançada verticalmente para cima, a partir do solo, tem sua altura h (em metros) expressa em função do tempo t (em segundos), decorrido após o lançamento, pela lei h(t) = 80t – 10t2. Determine a altura máxima atingida pela bola.
07 – Determine o valor máximo da função y = 50t – 0,25t2.
08 – Uma pequena fábrica vende seus bonés em pacotes com quantidades de unidades variáveis. O lucro obtido é dado pela expressão L(x) = –x2 + 12x – 20, onde x representa a quantidade de bonés contidos no pacote. A empresa pretende fazer um único tipo de empacotamento, obtendo um lucro máximo. Determine quantos bonés dever ser empacotados para que o lucro seja máximo.
Ufa!! Acabamos por aqui!
Lembrem-se de compartilhar essa atividade com seus colegas e com o seu professor.
Até a próxima, pessoal!!!

Excelentes atividades…. Apenas o vídeo apresentado não está relacionado com as atividades neste momento…. Seria interessante que os alunos assistissem vídeos sobre os vértices da parábola para responderem as atividades.
Todas as vídeo aulas tem acontecido em sincronia com as lista que chegam nas escolas.