Grandezas e Medidas – 5 ª Aula Matemática 6 ° Ano – 03/06/2020 - 03/06/2020
Olá pessoal! Vamos aprender hoje sobre Grandezas e Medidas.
Grandeza:
É tudo o que pode ser medido ou contado.
Vamos estudar grandezas em que basta um número e uma unidade de medida para defini-la. Podemos citar a medida de temperatura de uma febre de 40ºC, o tempo de caminhada de 30 minutos, a capacidade de 3 litros de água e a massa presente em 5 kg de arroz, como exemplos de grandezas com essas características.
Medida
Quando comparamos duas grandezas de mesma espécie, o resultado é uma medida.
Veja os vídeos a seguir explicando melhor sobre medidas.
Para se obter uma medida confiável de uma grandeza, é preciso que a comparação tenha uma unidade padrão. Por exemplo, poderíamos medir o comprimento de uma sala usando o pé como referência. Só que as dimensões dos pés podem alterar a medida. Imagine um pé “grande”, de numeração 45, e um pé “pequeno”, de numeração 30. Para uma medida correspondendo a uma numeração 900, seriam necessários 20 pés grandes (20 x 45 = 900), e seriam necessários 30 pés pequenos (30 x 30 = 900).
E agora, são 20 pés ou 30 pés?
Para resolver este problema, foi estabelecido que a medida padrão para comprimento é o metro. Então, podemos usar até formas diferentes para medir como a régua, a trena, o passo, ou o palmo, mas, ao compararmos esse comprimento com o comprimento de 1 metro, obteremos as mesmas medidas em metros.
Dizemos que os instrumentos régua e trena são padronizados, pois já contêm como referência, a unidade padrão. O palmo e o passo são unidades de medida não padronizadas.

Comprimento:
É a grandeza associada a extensão longitudinal entre dois pontos. Em termos mais simples, é a grandeza que pode ser medida, calculando-se a distância entre os dois pontos dados e comparando com a unidade de medida padrão de comprimento: o metro.
A seguir, temos uma tabela com o metro (m), seus múltiplos – quilômetro (km), hectômetro (hm) e decâmetro (dam) – e submúltiplos – decímetro (dm), centímetro (cm) e milímetro (mm).

Exemplo 1. De um submúltiplo (mm) a um múltiplo (km) – divisões sucessivas por 10.
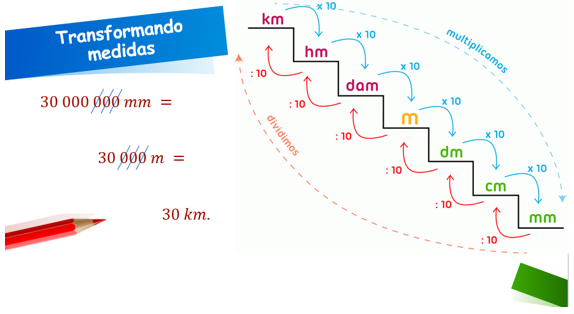
Exemplo 2. De um múltiplo (km) a um submúltiplo (cm) – multiplicações sucessivas por 10.
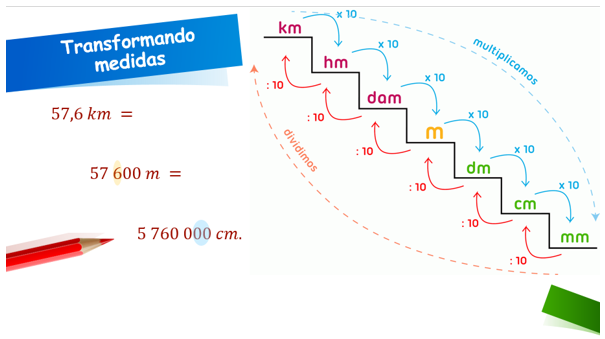
Exemplo 3. Perceba que as transformações fazem cortes de zeros ou deslocamentos de vírgula. Veja:
Note que se pode apenas deslocar a vírgula para a direita (ao multiplicar por 10) ou para a esquerda (ao dividir por 10), ou ainda, equivalentemente, acrescentar ou cancelar zeros para realizar as transformações, como segue nos exemplos a seguir:
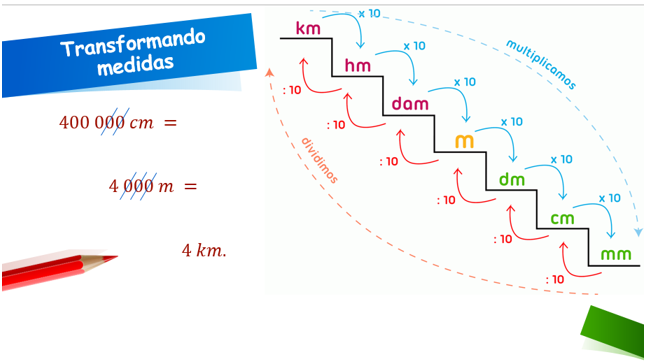
Exemplo 4. Deslocamento de vírgula.

Exemplo 5. Cortes de zeros.

Área
É a grandeza associada a extensão da região de um plano ou de uma superfície curva delimitada por uma linha fechada simples. É a grandeza associada à medida da superfície, e para os cálculos exigem-se duas dimensões. A unidade padrão de área é o metro quadrado.
A partir do metro quadrado (m²), temos seus múltiplos – quilômetro quadrado (km²), hectômetro quadrado (hm²) e decâmetro quadrado (dam²) – e seus submúltiplos – decímetro quadrado (dm²), centímetro quadrado (cm²) e milímetro quadrado (mm²).
Para a transformação das unidades de área, usamos a tabela a seguir:
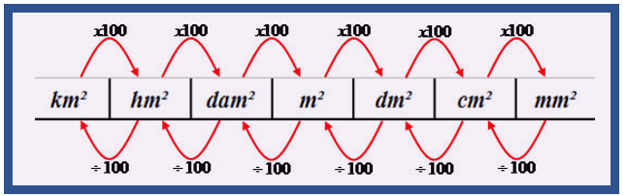
Exemplo 1. Para transformar uma unidade de área para outra, deslocando-se para a direita, deve-se multiplicar por 100 a cada unidade deslocada. Veja:
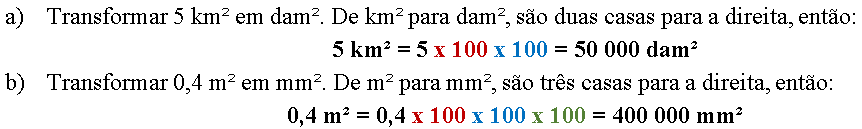
Exemplo 2. Para transformar uma unidade de área para outra, deslocando-se para a esquerda, deve-se dividir por 100 a cada unidade deslocada. Veja:

Volume:
É a grandeza indicada pela medida do espaço que um corpo ocupa, isto é, uma medida em três dimensões. A unidade padrão de volume é o metro cúbico, medida que indica o espaço ocupado por um corpo de dimensões 1 metro de comprimento, 1 metro de largura e 1 metro de altura.
A partir do metro cúbico (m³), temos seus múltiplos – quilômetro cúbico (km³), hectômetro cúbico (hm³) e decâmetro cúbico (dam³) – e seus submúltiplos – decímetro cúbico (dm³), centímetro cúbico (cm³) e milímetro cúbico (mm³). Para a transformação das unidades de volume, usamos a tabela a seguir:

Exemplo 1. Para transformar uma unidade de volume para outra, deslocando-se para a direita, deve-se multiplicar por 1 000 a cada unidade deslocada. Veja:

Exemplo 2. Para transformar uma unidade de volume para outra, deslocando-se para a esquerda, deve-se dividir por 1 000 a cada unidade deslocada. Veja:

Capacidade:
É a grandeza que estima a quantidade de líquido que ocupa um determinado recipiente. A unidade padrão de capacidade é o litro.
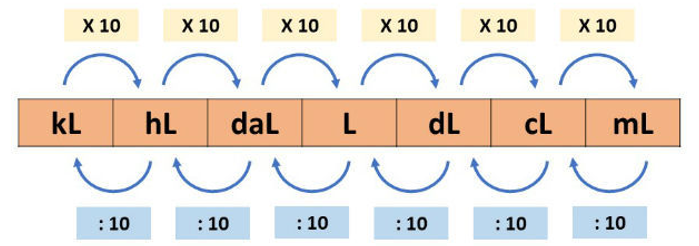
A partir do litro (L), temos seus múltiplos – quilolitro (kL), hectolitro (hL) e decalitro (daL) – e seus submúltiplos – decilitro (dL), centilitro (cL) e mililitro (mL).
Para a transformação das unidades de capacidade, usamos a tabela a seguir:
Exemplo. Um carregamento de 20 caixas, cada uma contendo 6 garrafinhas de refrigerante com capacidade de 200 mL, chegou no Armazém das Capacidades. Qual é a medida desse carregamento, em litros?
Solução. Multiplicando-se a quantidade de caixas pela quantidade de garrafinhas por caixa e pela capacidade de cada uma em mL, temos:
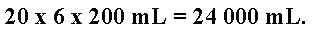
De mL para L, seguindo a tabela, são três casas para a esquerda. Dessa forma, podemos dividir por 10 a cada casa deslocada, ou ainda, deslocar com a vírgula três casas para a esquerda, ou apenas, cancelar três zeros, assim como fizemos para as medidas de comprimento.
Veja que dividir por 1000 (dividir por 10 e por 10 e por 10); deslocar a vírgula para a esquerda três casas ou simplesmente cancelar os três zeros, são maneiras equivalentes de se obter a mesma resposta:
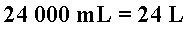
Veja que a grandeza capacidade é específica para os estudos envolvendo o preenchimento de recipientes ou reservatórios no espaço, com líquidos. Volume é a grandeza que exprime a medida do espaço, que pode estar inicialmente vazio, ou ainda, preenchido com materiais sólidos, líquidos ou gasosos. No caso específico dos líquidos, como por exemplo a água, eles assumem a mesma forma que os recipientes que os contém, e por essa razão, podemos associar as medidas de capacidade com as de volume por meio das seguintes relações:

Pratique agora em seu caderno com os próximos exercícios.
1. Reescreva cada uma das medidas a seguir na unidade pedida.
a) 230 m em centímetros =
b) 4,65 km em decímetros =
c) 1,9 cm em decâmetros =
d) 51,76 mm em metros =
2. Realize as conversões entre as medidas a seguir.
a) 12,3 km² em m² =
b) 0,25 cm² em mm² =
c) 14,36 m² em cm² =
d) 8.749,2 mm² em m² =
e) 5,29 m³ em dm³ =
f) 475,1 cm³ em m³ =
g) 91,002 mm³ em dm³ =
h) 0,005 dm³ em mm³ =
3. Calcule o valor das seguintes expressões dando a resposta em metros.
a) 25 dm + 8 m =
b) 12 cm + 301 mm + 1 dm =
c) 24 dam – 30 dm =
d) 125 mm + 60 cm + 71 dm =
e) 14 hm + 21 cm – 5 dam =
f) 3 km – 4 hm + 3 dam – 2 m =
4. Observe a figura a seguir.
Trata-se de um quadrado de lado 4 metros. Calculando-se a soma das medidas de seus 4 lados, ou seja, calculando seu perímetro, obtemos 16 metros.
Se as medidas dos lados forem dobradas, a medida do perímetro também será dobrada? Justifique sua resposta.
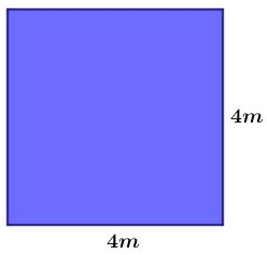
5. Qual é a medida da área, em centímetros quadrados, de uma sala de aula retangular cujas medidas são 8 m de largura por 10 m de comprimento? Lembre-se que a área do retângulo é dada pelo produto de suas dimensões.
6. Foi feita a medição do comprimento da parede de uma sala, utilizando, como instrumento de medida, uma fita métrica de apenas 80 cm. Essa medição correspondeu a 5 medidas e meia da fita.
Quantos metros de comprimento tem a parede?
(A) 4,4 m
(B) 4,5 m
(C) 8,0 m
(D) 8,5 m
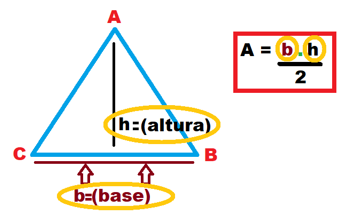
7. Sabe-se que a área de um triângulo é igual à metade do produto entre as medidas de sua base e da altura relativa a essa base, como ilustra a imagem. Qual é a medida da área de um triângulo, em metros quadrados, com base de medida igual a 80 cm e altura de medida igual a 125 cm?
(A) 0,25
(B) 0,50
(C) 1,00
(D) 1,25
8. O Aterro Sanitário de Gramacho chegou a possuir incríveis 1,3 milhões de metros quadrados. Em quilômetros quadrados, a área do “lixão” de Gramacho corresponde a:
(A) 1 300.
(B) 1,3.
(C) 1 300 000.
(D) 130 000.
9. Veja o paralelepípedo a seguir.
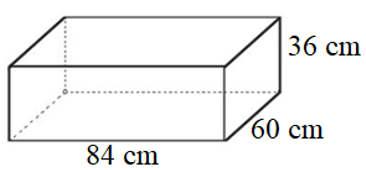
Qual a capacidade, em litros, desse paralelepípedo?
Lembre-se que o volume do paralelepípedo (V) é dado pelo produto de suas três dimensões, isto é,
V = comprimento x largura x altura
Ufa!! Acabamos por aqui!
Lembrem-se de compartilhar essa atividade com seus colegas e com o seu professor.
Até a próxima, pessoal!!!

Gostei dessa matéria parece ser bem fácil