Fala galerinha! Vamos aprender hoje sobre Princípio multiplicativo da contagem.

O princípio multiplicativo constitui a ferramenta básica para resolver problemas de contagem sem que seja necessário enumerar seus elementos.

Contar objetos é uma ação simples e natural, porém, há situações em que a contagem normal pode ser demorada ou até mesmo incompatível com o que queremos contar, como no caso das possibilidades onde teremos que agrupar e combinar de todas as formas possíveis elementos de conjuntos diferentes. Aprendemos formas de determinar quantas são as possibilidades ou combinações de uma dada situação usando o Princípio Multiplicativo da contagem e a forma de organizar e representar quais são todas elas.

Veja o vídeo a seguir explicando melhor sobre o assunto.

Veja os exemplos a seguir:

Exemplo 01

Daniel tem em mãos 3 fichas de cartolina vermelha com os números 1, 2 e 3 e quatro fichas de cartolina verde com números 1, 2, 3 e 4. Ele pretende encontrar quantos e quais são, todos os agrupamentos de 2 fichas onde a primeira é vermelha e a segunda é verde.

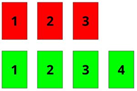
Com o auxílio de uma tabela de dupla entrada, vamos ajudar Daniel a organizar seu raciocínio para obter a lista de todos os agrupamentos possíveis que quer fazer, bem como saber quantos são eles.

Primeiramente, vamos determinar o número de agrupamentos que devemos obter aplicando o Princípio Multiplicativo da Contagem.

Temos 3 fichas vermelhas e 4 fichas verdes, logo 3 . 4 = 12 ou seja, a tabela deve oferecer 12 agrupamentos apresentados na tabela a seguir.

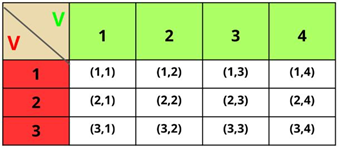
Exemplo 02

Bia vai sair com suas amigas e, para escolher a roupa que usará, separou 2 calças e 3 camisetas. Vejamos de quantas maneiras ela pode se arrumar.

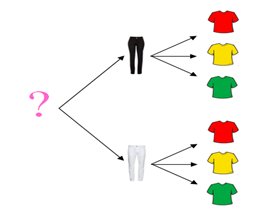
 O princípio multiplicativo, ilustrado nesse exemplo, também pode ser enunciado da seguinte forma: Se uma decisão d1 pode ser tomada de n maneiras e, em seguida outra decisão d2 puder ser tomada de mmaneiras, o número total de maneira de tornarmos as decisões d1 e d2 será n.m.

No exemplo anterior havia duas decisões a serem tomadas:

d1: escolher uma dentre as 3 blusas

d2: escolher uma dentre as 2 calças

Assim Bia dispõe de 3 . 2 = 6 maneiras diferentes de tomar decisões d1 e d2, ou seja, 6 possibilidades diferentes de se vestir.

Exemplo 03

Um restaurante prepara 4 tipos de pratos quentes (frango, peixe, carne assada, salsichão), 2 saladas (verde e russa) e 3 sobremesas (sorvete, romeu e julieta, frutas). De quantas maneiras diferentes um freguês pode se servir consumindo um prato quente uma salada e uma sobremesa?

Observe que nesse problema temos três níveis de decisão:

d1: escolher um dentre os 4 tipos de pratos quentes

d2: escolher uma dentre as 2 variedades de salada

d3: escolher uma dentre as 3 sobremesas oferecidas

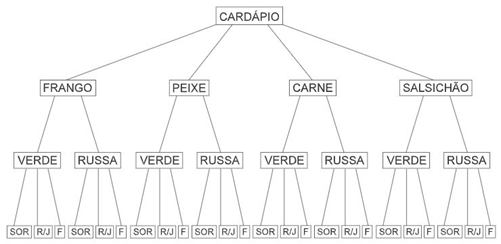
Usando o princípio multiplicativo, concluímos que temos 4 . 2 . 3 = 24 maneiras de tomarmos as três decisões, ou seja, 24 opções de cardápio. Veja a seguir como pode ser representado pela árvore de possibilidades ou grafo.

Vamos praticar! Resolva os exercícios em seu caderno.

01. De quantas maneiras podemos escolher um gerente, um tesoureiro e um secretário para uma empresa, sendo que há 10 candidatos a gerente, 20 candidatos a tesoureiro e 30 candidatos a secretário?

02. De quantas maneiras podemos escolher um capitão, um imediato e um timoneiro de bordo de uma tripulação composta por 15 homens?

03. Fernando planeja ir à praia e deseja utilizar uma camiseta e uma bermuda. Sabe-se que ele possui 2 camisetas e 3 bermudas. De quantas maneiras distintas Fernando poderá vestir-se? Utilize desenho para representar as possibilidades, conforme foi feito no exemplo 2.

04. Um jogo possui 6 cartas verdes, 3 cartas vermelhas. Quantas agrupamentos de 2 cartas são possíveis combinar? Represente em forma de tabela.

5. Uma lanchonete oferece no cardápio 4 tipos sanduíches (bacon, tudo, simples, especial), 3 saladas distintas (alface, tomate, rúcula), 2 variedades de bebidas (uva, cola). Uma pessoa deseja uma salada, um sanduiche, uma bebida. De quantas maneiras a pessoa poderá fazer seu pedido? Represente em forma de árvore de possibilidades.

06. Quantos números de 3 algarismos distintos podemos formar empregando os caracteres 1, 3, 5, 6, 8 e 9?

Ufa!! Acabamos por aqui!

Lembrem-se de compartilhar essa atividade com seus colegas e com o seu professor.

Até a próxima, pessoal!!!