Olá pessoal! Vamos aprender hoje sobre Grandezas e Medidas.

Definimos por grandeza tudo aquilo que pode ser contado e medido, como o tempo, a velocidade, comprimento, preço, idade, temperatura entre outros. As grandezas são classificadas em: diretamente proporcionais e inversamente proporcionais.

Veja o vídeo a seguir explicando sobre grandezas diretamente e inversamente proporcionais

Grandezas diretamente proporcionais são aquelas grandezas onde a variação de uma provoca a variação da outra numa mesma razão. Se uma dobra a outra dobra, se uma triplica a outra triplica, se uma é dividida em duas partes iguais a outra também é dividida à metade. Antes de chegar à definição de proporcionalidade direta é necessário saber alguns conceitos.

1. Razão entre duas grandezas a e b é a relação que existe entre elas e representa-se por (razão de a para b). Os números a e b são termos da razão, a é o antecedente e b o consequente.

2. Equivalência   de   razões: obtém-se   uma   razão   equivalente   a   uma   razão   dada, multiplicando ou dividindo ambos os termos da razão dada por um número diferente de zero. Veja uma relação de equivalência:

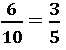
Veja: ao multiplicar o numerador e denominador por  temos:

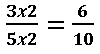
3. Proporção é uma igualdade entre duas razões. Em qualquer proporção o produto dos meios é igual ao produto dos extremos. Na proporção 3/5=6/10 onde 3 e 10 são os extremos e 5 e 6 são os meios. Então 3×10 = 5×6, logo temos que: 30=30.

4. Regra de Três é um método prático para resolver problemas que envolvem duas grandezas direta ou inversamente proporcionais.

Veja alguns passos para você seguir ao se deparar com um problema de proporcionalidade direta ou inversa.

1. Construa uma tabela, agrupando as grandezas da mesma espécie em colunas e mantendo na linha as grandezas de espécies diferentes em correspondência.

2. Identifique se as grandezas são diretamente ou inversamente proporcionais.

3. Monte a proporção e resolva a equação.

EXEMPLO 1

A Maria foi ao mercado fazer compras e comprou batatas que estavam em promoção, como mostra a figura.

Quanto ela pagaria por 12 kg de batatas?

Resolução:

1) Construção da tabela:

Se 6 kg custa, R$ 9,00, aumentando a quantidade, vai aumentar, também o valor a ser pago. Logo, as grandezas são diretamente proporcionais.

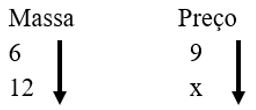
2) Resolução da equação;

Vamos aplicar a regra de proporção (regra de três).
Quando as grandezas são diretamente proporcionais, basta fazer a “multiplicação cruzada” ⇒ 6 .x = 12 .9

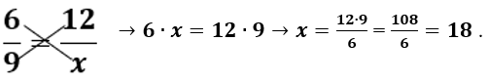
Portanto Maria pagaria R$ 18,00 por 12 kg de batatas.

Dadas as grandezas A e B, dizemos que elas são inversamente proporcionais quando um aumento na medida da grandeza A faz com que a medida da grandeza B diminua na mesma proporção, ou vice-versa.
Duas variáveis x e y são inversamente proporcionais, se o produto entre elas for uma constante não nula ou seja duas grandezas variáveis dependentes são inversamente proporcionais quando a razão entre os valores da 1ª grandeza é igual ao inverso da razão entre os valores correspondentes da segunda.

EXEMPLO 2

Um muro foi construído por 8 operários em 30 dias. Quantos dias seriam necessários para a construção deste mesmo muro, se fossem utilizados 12 operários?

Resolução:
Para resolver esse problema, podemos usar a regra de proporção (regra de três).

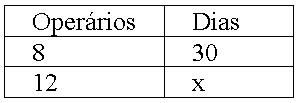
Observação:

Como as grandezas a serem comparadas são o número de funcionários e os dias de trabalho, se você aumentar a primeira, a segunda grandeza diminui. Então estamos lidando com grandezas inversamente proporcionais.
Uma maneira de resolver é utilizando o conceito de grandezas, que são inversamente proporcionais:
Assim: 8 .30=12.x ⇒x=20 dias
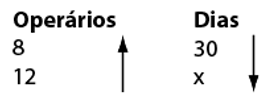
Outra forma é usar o recurso didático das flechas, como indicado acima. Se são inversamente proporcionais, as flechas são colocadas em sentido contrário.
A seguir temos uma proporção, onde manteve-se a fração onde se encontra a incógnita e inverteu-se a outra.

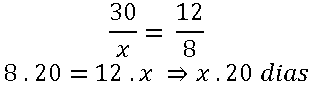
Logo, serão necessários 20 dias para a construção do muro, utilizando 12 operários.

Agora, para praticar resolva os seguintes exercícios no seu caderno.

1. Verifique se as proporções a seguir são verdadeiras.

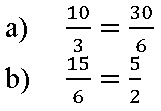
2. Determine o valor do termo representado pela incógnita nas proporções a seguir.

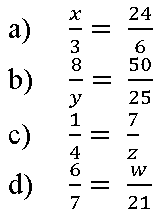
3. Em uma maquete de um condomínio, um de seus prédios de 80 metros de altura está com apenas 48 centímetros. A altura de um outro prédio de 110 metros nessa maquete, mantidas as devidas proporções, em centímetros, será de:

(A) 56

(B) 60

(C) 66

(D) 72

4. Uma fábrica mantém jornadas de trabalho de 6 horas para seus funcionários e, com essa jornada, a produção mensal é de 160 produtos. Quantas horas diárias serão necessárias para elevar a produção para 240 produtos?

(A) 2 horas

(B) 4 horas

(C) 5 horas

(D) 9 horas

5. De acordo com o Censo realizado no Brasil em 2010, havia cerca de 48 homens para 50 mulheres. Sabendo-se que, ainda segundo essa pesquisa, havia aproximadamente 93,4 milhões de homens no Brasil, então o número de mulheres no Brasil, em 2010, era aproximadamente, em milhões:

(A) 87

(B) 89

(C) 95

(D) 97

6. Paulo Ricardo caminha 80 metros em 5 minutos. mantendo a velocidade, em 35 minutos terá percorrido:

(A) 500 metros.

(B) 520 metros.

(C) 560 metros.

(D) 580 metros.

7. Uma turma de 30 alunos quer comprar um presente para a professora de matemática no valor de R$ 120,00. Inicialmente não foram todos os alunos que concordaram em presentear a professora. Pergunta-se:

a) Se apenas 3 alunos participarem da vaquinha, quanto cada um deverá dar para comprar o presente?

b) E se forem apenas 4?

c) E se forem apenas 6?

d) E se forem apenas 8?

8. Um veículo com velocidade de 50 km/h faz um percurso em 4 horas. Qual seria a velocidade necessária para que esse veículo fizesse esse mesmo percurso em 2 horas?

9. Para encher um tanque são necessários 60 galões de 6 litros cada um. Se forem usados galões de 2 litros cada um, quantos serão necessários para encher esse tanque?

Ufa!! Acabamos por aqui!

Lembrem-se de compartilhar essa atividade com seus colegas e com o seu professor.

Até a próxima, pessoal!!!