Fala galera! Vamos aprender hoje sobre Racionalização de Denominadores.

O que existe em comum entre os pares de frações a seguir?

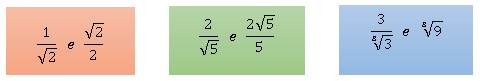
Elas são frações equivalentes. A racionalização de um denominador muitas vezes nos dá mais clareza do valor numérico de uma fração irracional. Mentalmente, costuma-se interpretar mais facilmente √2/2, que é aproximadamente 0,7, do que 1/√2.

Par encontrar uma fração equivalente de denominador racional, precisamos multiplicar os termos da fração por um mesmo número, que torne racional o denominador irracional. Vamos fazer um exemplo para que isso fique bem claro.

Veja o vídeo a seguir explicando melhor sobre o assunto.

Exemplos: Denominador do tipo √a.

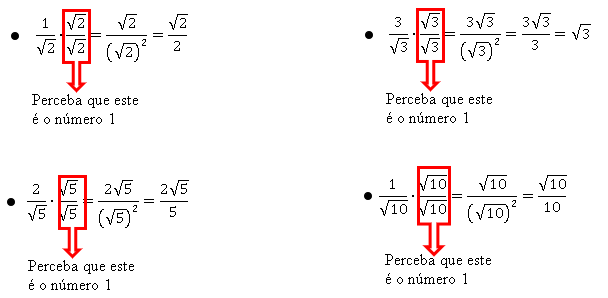
E se o denominador não for uma raiz quadrada, como faremos a racionalização?

Vamos observar a seguinte multiplicação:

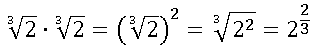
Perceba que não conseguimos tornar a raiz cúbica de 2 em um número racional, pois a multiplicação desse número por ele mesmo não gerou o resultado esperado. Como devemos fazer essa multiplicação?

Toda vez que o denominador for do tipo:

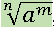
multiplicaremos esse valor por:

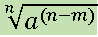
Exemplo:

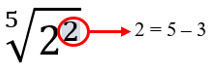
Logo,

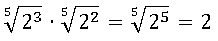
Como representar um número irracional na reta numérica?

Os números irracionais são decimais infinitos e aperiódicos. Assim, para representá-los na reta numérica, podemos aproximá-los por um número racional.

Vamos determinar uma aproximação para √5.

I. Primeiro identificaremos entre quais número racionais o valor se encontra, utilizando os dois quadrados perfeitos entre os quais se encontra √5

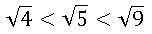
Assim, 2 < √5 < 3.

II. Vamos aproximar √5 por um número racional com uma casa decimal.

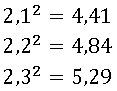
A partir dos cálculos acima, verificamos que √5≅2,2. Dizemos que o valor de √5 com erro menor que 0,1 é 2,2. Na reta numérica, temos?

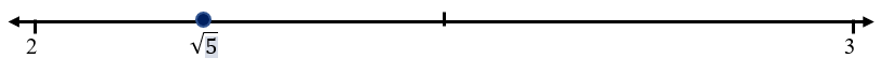
III. Para determinar o valor de √5 com erro menor que 0,01, devemos utilizar um número racional com duas casas decimais.

Como já sabemos que 2,2 < √5 < 2,3, temos:

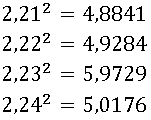
O valor de √5com erro menor que 0,01 é 2,23.

O valor aproximado de uma raiz não exata é aquele mais próximo que não excede o valor da raiz. Logo, √5≅2,23 e não igual a 2,23

Determinar o valor aproximado da raiz quadrada de um número N qualquer.

Um método heurístico de calcular a aproximação para raízes quadradas é através da fórmula abaixo:

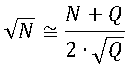
Onde Q é o número quadrado perfeito mais próximo de N. Utilizando esta fórmula, qual a melhor aproximação para √50.

Perceba que Q = 49, logo:

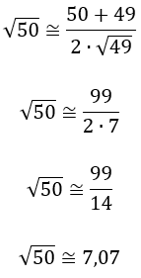
Agora pratique resolvendo os seguintes exercícios no caderno.

01. Associe as frações da coluna (I), com suas respectivas frações equivalentes na coluna (II).

02. Substitua o símbolo # por um fator não nulo que torne o produto um número racional.

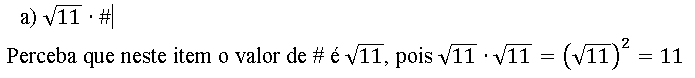
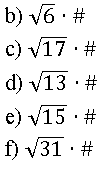
03. Substitua o símbolo # por um fator não nulo que torne o produto um número racional.

05. Represente na reta numérica os seguintes números, √7,√11 e √20, e determine o seu valor aproximado com um erro de 0,01.

06. Utilizando o método heurístico, calcule a raiz aproximada dos seguintes números.

07. A figura a seguir representa uma sala.

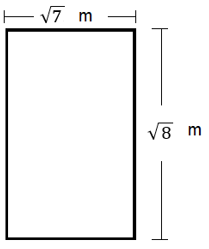
Qual a área dessa sala, aproximadamente? Use o método heurístico.

Ufa!! Acabamos por aqui!

Lembrem-se de compartilhar essa atividade com seus colegas e com o seu professor.

Até a próxima, pessoal!!!