Razões Trigonométricas no Triângulo Retângulo – 9º Ano – 3ª quinzena – 3º corte – AULA e IMPRESSÃO - 30/09/2020
 VAMOS INICIAR NOSSA ATIVIDADE!!!
VAMOS INICIAR NOSSA ATIVIDADE!!!
INTRODUÇÃO À TRIGONOMETRIA
Os povos antigos tinham a necessidade de medir distâncias, alturas, áreas e volumes. A trigonometria surgiu como uma relação entre determinadas medidas em função dos ângulos que as relacionavam.
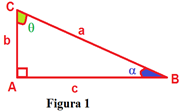
Para iniciarmos nosso estudo utilizaremos o triângulo retângulo a seguir.
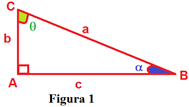
Sabemos que o ângulo  vale 90º e que o lado oposto a ele é chamado de hipotenusa e tem medida representada por “a”. Os demais lados são chamados de catetos, ou seja e e suas medidas são representadas por “b” e “c” respectivamente.
Como a soma dos ângulos internos de um triângulo é 180º , temos portanto que α e somados valem 90º , ou seja, α + ϴ = 90º e então são ditos complementares.
Como temos um triângulos retângulo, não podemos deixar de lembrar do Teorema de Pitágoras:

Dizemos que um triângulo retângulo é Pitagórico, se as medidas de seus lados são números inteiros positivos. O exemplo clássico desse triângulo é o triângulo 3; 4; 5, ou seja, os catetos medem 3 e 4, e sua hipotenusa vale 5.
Chamamos de cateto oposto, o cateto que está de frente para o ângulo. Em relação a “α”, o cateto “b” é oposto e, em relação a “ ” o cateto “c” é o seu oposto.
Chamamos de cateto adjacente, o cateto que é lado do ângulo, ou seja, estar adjacente significa estar ao lado. Em relação a “α”, o cateto “c” é adjacente e, em relação a “ ” o cateto “b” é o adjacente.
Estudo do Seno, cosseno e tangente
Definimos como Seno de um ângulo, o quociente (divisão) entre a medida do cateto oposto a esse ângulo e a medida da hipotenusa do triângulo retângulo, logo:



Atividades
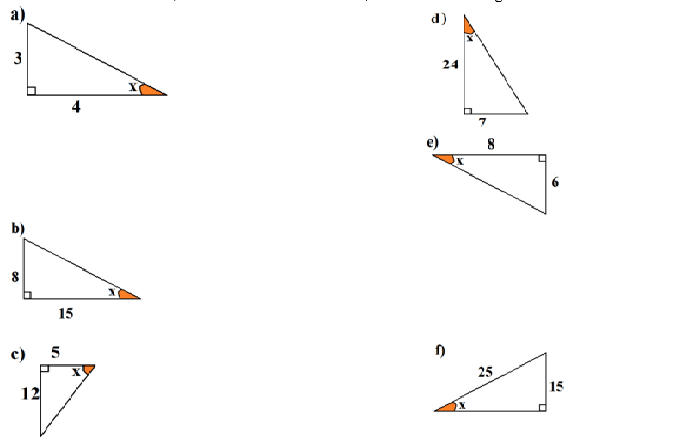
1) Em cada um dos triângulos pitagóricos a seguir, existe uma medida de lado que está faltando. Calcule a medida desse lado e então, determine os valores do seno, do cosseno e da tangente de x em cada caso:
2) Observe o quadrado ABCD da figura a seguir.
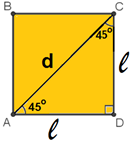
a) Determine a medida de sua diagonal em função da medida de seu lado “l”.
b) Determine os valores do seno, do cosseno e da tangente do ângulo de 45º.
3) Observe o triângulo equilátero ABC, de lado “l” a seguir.
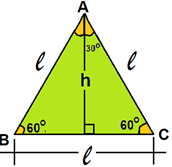
- Calcule a medida de sua altura “h” em função do lado do triângulo.
- Determine os valores do seno, do cosseno e da tangente dos ângulos de 30º e 60º .
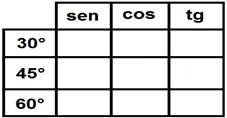
4) Os valores do seno, do cosseno e da tangente dos ângulos de 30º, 45º e 60, na trigonometria, são chamados de valores notáveis. Dessa forma, complete a tabela de valores notáveis.
5) Um observador está no ponto A e visualiza o topo de um prédio (ponto B) sob um ângulo de 30º conforme a figura a seguir.
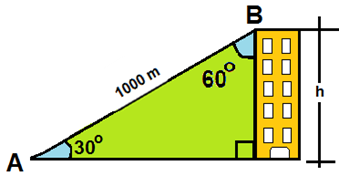
Desprezando a altura do observador pode-se afirmar que a altura do prédio está entre:
a) ( ) 481 e 510 metros.
b) ( ) 511 e 540 metros.
c) ( ) 541 e 570 metros.
d) ( ) 571 e 601 metros.
6) A entrada de uma determinada escola possui dois degraus iguais com 15 cm de altura cada um. Pretende-se construir uma rampa para garantir a acessibilidade a todos, como mostra a figura a seguir.
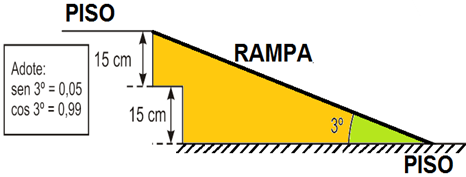
Qual o comprimento dessa rampa, sabendo que ela formará com o solo um ângulo de 3°?
a) ( ) 6 m.
b) ( ) 5 m.
c) ( ) 4 m. d) ( ) 3 m.
7) O Capitão América irá lançar seu escudo em uma inclinação em relação ao solo sob um ângulo de 60º, conforme a figura a seguir.
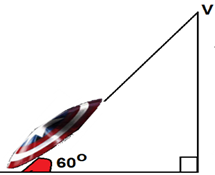
O Capitão pretende que seu escudo percorra a distância de 120 metros e, então atingirá um vilão no ponto V. Nestas condições, a altura em que se encontra o vilão é
a) ( ) 60 metros.
b) ( ) 120 metros.
c) ( ) 60√3 metros.
d) ( ) 120√3 metros.
8) A batnave, ao decolar da batcaverna, percorre uma trajetória retilínea formando um ângulo constante de 30º com o solo. Depois de percorrer 5.000 metros, nesta trajetória, a altura atingida pela aeronave do Batman, em metros, é
a) ( ) 1500.
b) ( ) 2000.
c) ( ) 2500
d) ( ) 3000.
Texto das questões 9 e 10.
Determinação da distância entre dois pontos no plano cartesiano.
Considere o plano cartesiano e os pontos A(xa,ya) e B(xb, yb). A medida do segmento que une esses pontos é chamada de distância entre A e B.
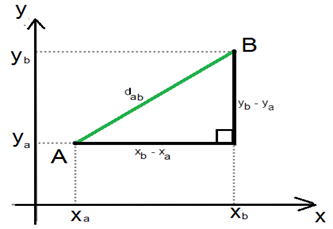
A distância entre os pontos A e B é a hipotenusa do triângulo retângulo formado por catetos “xb – xa” e “yb – ya”.
Aplicando o teorema de Pitágoras temos:
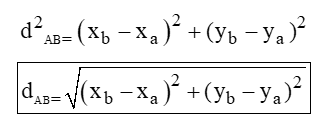
Portanto, a distância entre os pontos A(xa, ya) e B(xb, yb) é definida pelo comprimento do segmento representado por dAB e tem medida dada por:
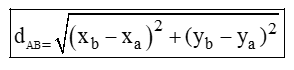
O ponto médio de um segmento
As coordenadas do ponto médio do segmento AB é calculado fazendo a média aritmética das coordenadas, ou seja;
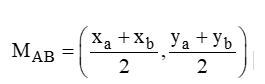
Exemplo:
Dados os pontos A (1, 3) e Q (7, 11), determine:
a) A distância entre eles;
b) As coordenadas do ponto médio entre eles.
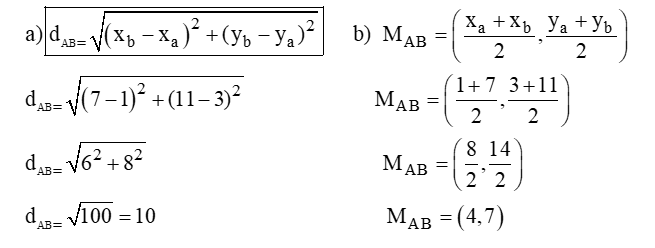
9) Dados os pontos nos itens abaixo, determine a distância entre eles e as coordenadas do ponto médio entre eles.
a) A(2,2) e B(5,6);
b) C(9,2) e D(4, -10).
10) Sabemos que um triângulo é isósceles se dois de seus três lados possuírem medidas iguais.
Dado o triângulo ABC no plano cartesiano a seguir.
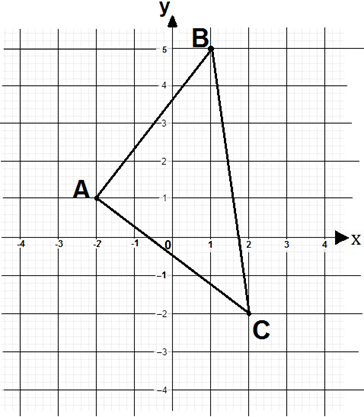
- Calcule as medidas de seus lados.
- Verifique se é isósceles.
 Concluímos…vamos revisar!!!
Concluímos…vamos revisar!!!
 Baixe e imprima sua atividade!
Baixe e imprima sua atividade!
9o-MAT-3aquinzena-3o-corteBaixar