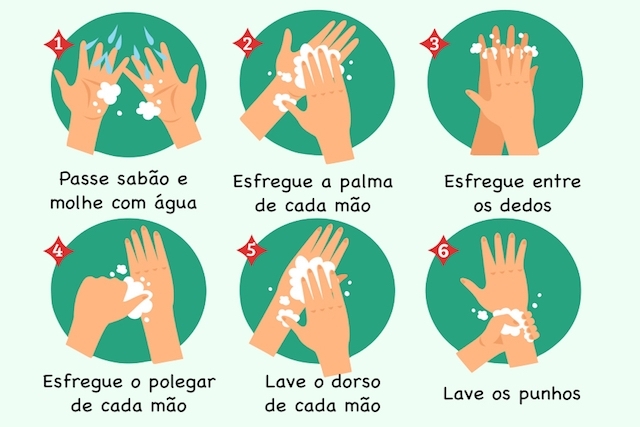
Retas paralelas cortadas por uma transversal – 7 ª Aula Matemática 9 ° Ano – 17/06/2020 - 18/06/2020
Olá pessoal! Vamos aprender sobre Retas paralelas cortadas por uma transversal?
Retas paralelas são aquelas que não se interceptam em nenhum ponto. Uma reta é transversal à outra se ambas apresentam apenas um ponto em comum. Ao traçarmos duas retas r e s, tal que r // s (r é paralela a s), e também uma reta transversal t que intercepte r e s, formara oito ângulos.
Veja o vídeo a seguir explicando sobre:
Observe a imagem a seguir.

A interseção da reta t com as retas paralelas r e s deu origem aos ângulos a, b, c, d, e, f, g e h. Podemos classificar os ângulos formados por duas retas paralelas cortadas por uma transversal de acordo com a posição desses ângulos. Se eles estiverem entre as retas paralelas, dizemos que esses ângulos são internos; caso contrário, dizemos que eles são externos. Ao analisarmos dois ângulos, eles podem estar do mesmo lado ou em lados alternados em relação à reta transversal. Se dois ângulos estão à direita ou ambos estão à esquerda da reta t, dizemos que esses ângulos são colaterais; mas se estão em lados alternados, um à direita, e o outro à esquerda, dizemos que esses ângulos são alternos.
Os ângulos podem ser classificados como internos ou externos, e dois ângulos podem ser colaterais ou alternos.

Ângulos alternos internos

Note que o ângulo d é congruente com o ângulo f e o ângulo e é congruente com o ângulo c, ou seja:

Ângulos alternos externos

Note que o ângulo a é congruente com o ângulo g e o ângulo b é congruente com o ângulo h, ou seja:

Exemplo 01.
Determine o valor real de x, sabendo que r//s.

Perceba que os ângulos 3x + 15º e x + 75º são alternos externos portanto:
3x + 15º = x + 75º
resolvendo a equação temos:
3x – x = 75º – 15º
2x = 60º
x = 30º
Ângulos colaterais internos

Note que o ângulo d e o ângulo e são suplementares, assim como os ângulos c e f, ou seja:

Ângulos colaterais externos

Note que o ângulo a e o ângulo h são suplementares, assim como osângulos b e g, ou seja:

Exemplo 02.
Determine o valor real de x, sabendo que r//s.

Perceba que os ângulos 3x + 15º e x + 25º são colaterais internos portanto:
3x + 15º + x + 25º = 180º
resolvendo a equação temos?
4x + 40º = 180º
4x = 180º – 40º
4x = 140º
x = 35º
Hora de praticar! Resolva os seguintes exercícios em seu caderno.
1. Determine o valor real de x, sabendo que r//s.

2. As retas r e s da figura são paralelas cortadas pela transversal t. Se a medida do ângulo B é o triplo da medida do ângulo A, então B – A vale:

3. Duas retas paralelas cortadas por uma transversal formaram um par de ângulos alternos internos representados por: 2x – 45º e x + 22º. Determine o valor de x e a medida de desses ângulos.
4. Dois ângulos colaterais internos foram formados quanto traçamos duas restas paralelas cortadas por uma transversal. Sabendo que esses ângulos são representados por A = 3x + 25º e B = 2x + 45º, determine o valor dos ângulos A e B.
5. Duas retas paralelas são cortadas por uma transversal, então a afirmativa FALSA é:
a) Os ângulos colaterais internos são congruentes.
b) Os ângulos correspondentes são congruentes.
c) Os ângulos alternos internos são congruentes.
d) Os ângulos alternos externos são congruentes.
e) Os ângulos colaterais externos não são congruentes.
6. Duas retas paralelas cortadas por uma transversal formam dois ângulos colaterais externos, de medidas 3x + 30º e 7x + 50°. Calcule a medida do ângulo agudo.
7. Duas retas formam, com uma transversal, ângulos alternos internos, expressos em graus por 7x – 1° e 4x + 5º. Calcule o valor de x, a fim de que essas retas sejam paralelas.
8. Na figura abaixo as retas r e s são paralelas. Os ângulos de medidas 60º e 120º são.

a) congruentes, pois são colaterais internos.
b) congruentes, pois são correspondentes.
c) congruentes, pois são alternos internos.
d) suplementares, pois são colaterais internos.
e) suplementares, pois são colaterais externos
Ufa!! Acabamos por aqui!
Lembrem-se de compartilhar essa atividade com seus colegas e com o seu professor.
Até a próxima, pessoal!!!