Transformações geométricas de polígonos no plano cartesiano – 7 ª Aula Matemática 7 ° Ano – 17/06/2020 - 18/06/2020
Olá pessoal! Vamos aprender sobre Transformações geométricas de polígonos no plano cartesiano?
TRANSFORMAÇÕES GEOMÉTRICAS DE POLÍGONOS NO PLANO CARTESIANO
Nessa aula trataremos sobre as transformações geométricas de polígonos no plano cartesiano decorrentes da multiplicação das coordenadas de seus vértices por um número inteiro. Para conseguir entender sobre esse assunto, vamos relembrar alguns conceitos. A palavra “geometria” tem origem grega e sua tradução literal é: “medir a terra”, nesse caso formas dos objetos presentes na natureza, das posições ocupadas por esses objetos, das relações e das propriedades relativas a essas formas, ela é construída sobre objetos primitivos: ponto, reta, plano, espaço, entre outros.
O ponto não possui forma nem dimensão. Um dos usos mais importantes do ponto refere-se à localização geográfica.
As retas são conjuntos de pontos que não fazem curvas.
Como esses pontos não estão no mesmo lugar, é possível medir a distância entre eles.
O plano é um conjunto de retas alinhadas e, portanto, também é um conjunto de pontos. O objeto formado por esse alinhamento de retas é uma superfície plana.
Plano cartesiano é um traçado de retas perpendiculares onde perpassa outra, sendo uma na horizontal e outra na vertical, formando quadrantes de 90°. Uma das principais partes que formam o plano cartesiano são os eixos, que são chamados de abscissas e ordenadas. Abscissa é uma coordenada na horizontal, geralmente denominada como X. A ordenada, que é o contrário da abscissa, é a linha vertical nomeada de Y.
Veja a representação nas imagens a seguir.
Como no plano cartesiano são duas retas numéricas onde as localizações dos pontos dependem da combinação de dois números reais, ou seja, de duas coordenadas (x,y), são divididos em quadrantes. Quando temos um ponto (x,y), determinamos seus simétricos. Para isso precisamos primeiro escrever as coordenadas de cada um dos pontos marcados nesse plano cartesiano. Veja a representação nas figuras a seguir.
Observe que os pontos marcados estão à esquerda do eixo y.
De acordo com as coordenadas dos vértices desse triângulo representado na Figura 2 vamos determinar o simétrico de cada um dos 3 pontos do polígono em relação ao eixo y desenhando o novo triângulo no 1º quadrante representado na Figura 3 que será simétrico ao polígono original, tendo em vista que multiplicamos a coordenada de x por (-1).
Veja no vídeo a seguir um exemplo.
Exemplo 2
O polígono nesse plano cartesiano tem como pares ordenados: A(2,3), B(4,5) e C(7,1) como podem observar na Figura 4. Note que para cada vértice existe um par ordenado.
Através da operação da multiplicação das coordenadas de seus vértices por um número inteiro pode-se obter transformações geométricas. Ao se multiplicar as coordenadas (x,y) do polígono representado no plano cartesiano anterior por (-1), se obtém uma alteração de quadrante da figura geométrica. Veja!

O polígono se encontra agora no 3º quadrante, como se vê representado na Figura 5.
Acompanhe o processo:
A(2,3)→2(-1),3(-1)=A´(-2,-3)
B(4,5)→ 4(-1),5(-1)=B´(-4,-5)
C(7,1)→ 7(-1),1(-1)=C´(-7,-1)
O polígono representado na Figura 5 é o reflexo do polígono representado na Figura 4 em relação a origem do plano cartesiano.
Exemplo 2
Ao multiplicarmos as coordenadas dos vértices de um polígono por um número inteiro obtemos um novo polígono que pode ser apenas a ampliação do primeiro ou ser a reflexão do mesmo em relação a origem.
O que podemos observar e relação ao 1º e ao 2º polígono?
Se olhar atentamente vai observar que os pares ordenados do 2º polígono são o dobro do 1º.
Acompanhe o processo:
(2,3)→2(2),3(2)=(4,6)
(4,5)→ 4(2),5(2)=(8,10)
(7,1)→ 7(2),1(2)=(14,2)
Hora de praticar! Resolva em seu caderno os seguintes exercícios.
1. Localize no plano cartesiano os seguintes pontos: A(2,3), B(-3,1) e C(3,-2).
2. No plano cartesiano abaixo temos a metade de uma figura. Determine as coordenadas dos pontos marcados no plano. Em seguida, marque o simétrico destes pontos em relação ao eixo y para desenhar a outra metade da figura.
3. Verifique quais são as coordenadas dos vértices do hexágono ao lado. Em seguida, determine o simétrico de cada um dos 6 pontos do polígono em relação ao eixo x. Desenhe o novo hexágono. Este será simétrico ao polígono original.
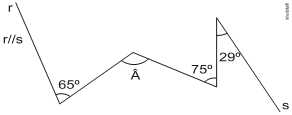
4. Determine o simétrico dos 3 pontos do triângulo em relação ao eixo y e desenhe o novo polígono. Em seguida, desenhe o simétrico do polígono em relação ao eixo x. Para terminarmos, marque o simétrico em relação à origem do plano cartesiano dos 3 pontos do polígono original e desenhe o novo triângulo.
5. Marque no plano cartesiano os vértices de um retângulo. As coordenadas são: A(1,1), B(5,1), C(1,4) e D(5,4). Este retângulo será desenhado no 1º quadrante. Em seguida, multiplique as coordenadas dos vértices do polígono pelo número inteiro ౼2 e marque as novas coordenadas no plano cartesiano formando um novo polígono. Verifique em qual quadrante ele se encontra e compare sua dimensão como a do polígono original.
6. Dados os pontos A(2,1); B(2,4); C(5,1) e D(5,4), marque-os no plano cartesiano e ligue-os formando um polígono. Em seguida, multiplique todas as coordenadas pelo número 2, formando 4 novos pontos. Marque esses pontos no plano cartesiano e ligue-os formando um novo polígono. Compare a área e o perímetro das duas figuras.
7. Dados os pontos A(౼3,2); B(౼8,2) e C(౼6,7), marque-os no plano cartesiano e ligue-os formando um polígono. Em seguida, multiplique todas as coordenadas por ౼1, formando 3 novos pontos. Marque esses pontos no plano cartesiano e ligue-os formando um novo polígono. O que você pode concluir analisando as duas figuras?
8. Dados os pontos A(౼2,2); B(౼4,1); C(౼6,3); D(౼5,5) e E(౼3,4), marque-os no plano cartesiano e ligue-os formando um polígono. Em seguida, multiplique todas as coordenadas pelo número ౼2, formando 5 novos pontos. Marque esses pontos no plano cartesiano e ligue-os formando um novo polígono. Analise as figuras, comparando a área e o perímetro das duas.
Ufa!! Acabamos por aqui!
Lembrem-se de compartilhar essa atividade com seus colegas e com o seu professor.
Até a próxima, pessoal!!!